题目内容
 (1)已知Rt△ABC的两条直角边AC=3cm,BC=4cm,则以直线BC为轴,旋转一周所得到的几何体的侧面积是
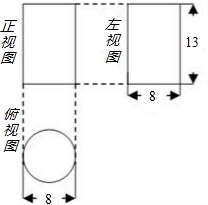
(1)已知Rt△ABC的两条直角边AC=3cm,BC=4cm,则以直线BC为轴,旋转一周所得到的几何体的侧面积是(2)如图是一个几何体的三视图,根据图示,可计算出该几何体的侧面积为
分析:(1)利用勾股定理易得圆锥的母线长,那么圆锥的侧面积=底面周长×母线长÷2;
(2)易得此几何体为圆柱,那么表面积=侧面积+两个底面积=底面周长×高+2πr2.
(2)易得此几何体为圆柱,那么表面积=侧面积+两个底面积=底面周长×高+2πr2.
解答:(1)两条直角边AC=3cm,BC=4cm,由勾股定理得,斜边AB=5,以直线BC为轴,旋转一周所得到的几何体得到一个圆锥,底面半径为AC=3,底面周长=6π,侧面面积=
×6π×5=15πcm2;
(2)由三视图得,几何体是圆柱,底面直径是8,高是13,则底面周长=8π,侧面面积=104πcm2.
| 1 |
| 2 |
(2)由三视图得,几何体是圆柱,底面直径是8,高是13,则底面周长=8π,侧面面积=104πcm2.
点评:本题利用了勾股定理,圆的周长公式,扇形的面积公式,矩形面积公式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 18、已知Rt△ABC中,∠B=90°.
18、已知Rt△ABC中,∠B=90°. B边上的点D、要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)
B边上的点D、要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)
 已知Rt△ABC中,∠A=90°,AC=8,BC=10,将△ABC沿直线ED折叠,使点B与点C重合,点A落在点F处,如图所示.
已知Rt△ABC中,∠A=90°,AC=8,BC=10,将△ABC沿直线ED折叠,使点B与点C重合,点A落在点F处,如图所示.