题目内容
给定整数n≥3,实数a1,a2,…,an满足min1≤i<j≤n|ai-aj|=1.求
|ak|3的最小值.
| n |
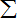 |
| k=1 |
不妨设a1<a2<…<an,则对1≤k≤n,有|ak|+|an-k+1|≥|an-k+1-ak|≥|n+1-2k|,
所以
|ak|3=
(|ak|3+|an+1-k|3)=
(|ak|+|an+1-k|)(
(|ak|-|an+1-k|)2+
(|ak|+|an+1-k|)2)≥
(|ak|+|an+1-k|)3≥
|n+1-2k|3.
当n为奇数时,
|n+1-2k|3=2•23•
i3=
(n2-1)2.
当n为偶数时,
|n+1-2k|3=2
(2i-1)3=2(
j3-
(2i)3)=
n2(n2-2).
所以,当n为奇数时,
|ak|3≥
(n2-1)2,当n为偶数时,
|ak|3≥
n2(n2-2),等号均在ai=i-
,i=1,2,n时成立.
因此,
|ak|3的最小值为
(n2-1)2(n为奇数),或者
n2(n2-2)(n为偶数).
所以
| n |
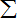 |
| k=1 |
| 1 |
| 2 |
| n |
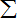 |
| k=1 |
| 1 |
| 2 |
| n |
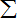 |
| k=1 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| n |
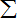 |
| k=1 |
| 1 |
| 8 |
| n |
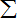 |
| k=1 |
当n为奇数时,
| n |
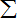 |
| k=1 |
| ||
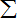 | ||
| i=1 |
| 1 |
| 4 |
当n为偶数时,
| n |
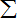 |
| k=1 |
| ||
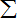 | ||
| i=1 |
| n |
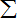 |
| j=1 |
| ||
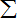 | ||
| i=1 |
| 1 |
| 4 |
所以,当n为奇数时,
| n |
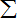 |
| k=1 |
| 1 |
| 32 |
| n |
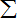 |
| k=1 |
| 1 |
| 32 |
| n+1 |
| 2 |
因此,
| n |
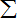 |
| k=1 |
| 1 |
| 32 |
| 1 |
| 32 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目