Question

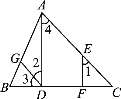
【题目】如图，将边长为6的正三角形纸片ABC按如下顺序进行两次折叠，展开后，得折痕AD、BE．(如图①)，点O为其交点．如图②，若P、N分别为BE、BC上的动点．如图③，若点Q在线段BO上，BQ=1，则QN+NP+PD的最小值=_______．

Answer 1

【答案】

【解析】

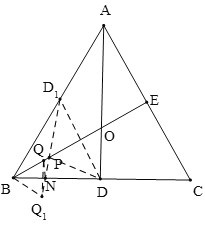
如图，作点Q关于BC的对称点Q1，点D关于BE的对称点D1，连接D1Q1，交BE于P，BC于N，连接BQ1，QN、PD，由等边三角形的性质和轴对称的性质可得∠CBE=∠Q1BN=∠ABE=30°，BQ=BQ1，BD=BD1，PD=PD1，NQ=NQ1，即可得Q1D1是QN+NP+PD的最小值，可得△BQ1Q和△BD1D是等边三角形，根据∠CBE=∠Q1BN=∠ABE=30°，可得∠ABQ1=90°，由AD是折痕可得BD=BC，利用勾股定理求出Q1D1的长即可得答案．

如图，作点Q关于BC的对称点Q1，点D关于BE的对称点D1，连接D1Q1，交BE于P，BC于N，连接BQ1，QN、PD，

∵△ABC是等边三角形，AD、BE是折痕，

∴∠CBE=∠Q1BN=∠ABE=30°，点D1在AB上，BD=BC=3，∠ABC=60°，

∴∠ABQ1=90°，∠Q1BQ=60°，

∵点Q关于BC的对称点D1，点D关于BE的对称点D1，

∴BQ=BQ1，BD=BD1，PD=PD1，NQ=NQ1，

∴△BQ1Q和△BD1D是等边三角形，Q1D1是QN+NP+PD的最小值，

∴BQ1=BQ=1，BD1=BD=3，

∴Q1D1==．

故答案为：