题目内容
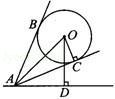
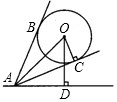 如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?(
如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?(| 3 |
分析:求OD就必须先求出OA,在直角三角形OAC中,易求得∠OAC=
∠BAC=30°,又知道OC=2,那么求出OA就不难了,有了OA的值在直角三角形OAD中便可求出OD的值了.
| 1 |
| 2 |
解答: 解:连接OB,则OB⊥AB,
解:连接OB,则OB⊥AB,
∴∠OBA=∠OCA=90°.
∵OB=OC,OA=OA,△OAB≌△OAC,∠OAB=∠OAC=30°,
直角三角形OAC中,OA=OC÷sin∠OAC=2OC=4m,
直角三角形OAD中,OD=OA•sin60°=2
≈3.46m.
因此OD的长时3.46m.
 解:连接OB,则OB⊥AB,
解:连接OB,则OB⊥AB,∴∠OBA=∠OCA=90°.
∵OB=OC,OA=OA,△OAB≌△OAC,∠OAB=∠OAC=30°,
直角三角形OAC中,OA=OC÷sin∠OAC=2OC=4m,
直角三角形OAD中,OD=OA•sin60°=2
| 3 |
因此OD的长时3.46m.
点评:本题考查全等三角形的判定与性质和解直角三角形的实际应用及分析问题、解决问题的能力.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?(
如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?( ≈1.73)
≈1.73)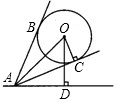
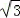 ≈1.73)
≈1.73)