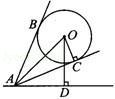
题目内容
如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?(
≈1.73)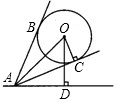
| 3 |


连接OB,则OB⊥AB,
∴∠OBA=∠OCA=90°.
∵OB=OC,OA=OA,△OAB≌△OAC,∠OAB=∠OAC=30°,
直角三角形OAC中,OA=OC÷sin∠OAC=2OC=4m,
直角三角形OAD中,OD=OA?sin60°=2
| 3 |
因此OD的长时3.46m.

练习册系列答案
相关题目
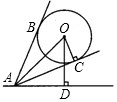 如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?(
如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?( 如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?(
如图,一个氢气球升在广场上空,已知氢气球的直径为4m,在地面上点A测得气球中心的仰角∠OAD=60°,测得气球的视角(两条视线AB,AC的夹角)∠BAC=60°,AC与圆相切于C,且OC⊥AC,则气球中心O离地面的高度OD为多少米?( ≈1.73)
≈1.73)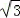 ≈1.73)
≈1.73)