题目内容
【题目】在直角坐标系中,(为坐标原点,点![]() ,点
,点![]() 是
是![]() 中点,连接(
中点,连接(![]() 将
将![]() 绕点
绕点![]() 顺时针旋转,得到
顺时针旋转,得到![]() ,记旋转角为
,记旋转角为![]() ,点
,点![]() 的对应点分别是
的对应点分别是![]() ,连接
,连接![]() 是
是![]() 中点,连接
中点,连接![]() .
.
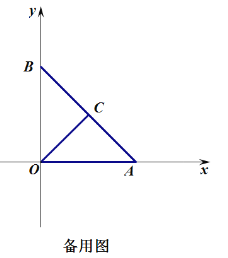
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;

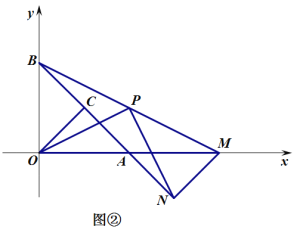
(2)如图②,当![]() 时,求证
时,求证![]() ,且
,且![]() ;
;
(3)当![]() 旋转至点
旋转至点![]() 共线时,求点
共线时,求点![]() 的坐标(直接写出结果即可) .
的坐标(直接写出结果即可) .
【答案】(1)点![]()
![]() ;(2)见解析;(3)点
;(2)见解析;(3)点![]() 或
或![]() .
.
【解析】
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由旋转图形性质,得到AM的长,再应用解直角三角形的知识问题可解;
,由旋转图形性质,得到AM的长,再应用解直角三角形的知识问题可解;
(2)根据直角三角形斜边上中线等于斜边一半可证OP=PN,再由三角形内角和知识,证明![]() 即可;
即可;
(3)根据题意画出满足条件图形,过M做![]() 于点E,利用锐角三角函数和旋转的知识,求出
于点E,利用锐角三角函数和旋转的知识,求出![]() ,则问题可解.
,则问题可解.
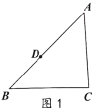
(1)如图![]() 点
点![]() ,点
,点![]()
![]()
![]() 是
是![]() 中点
中点
![]() ,
,
且![]()
即![]() 为等腰直角三角形
为等腰直角三角形
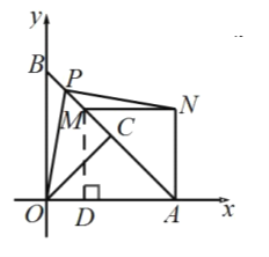
当![]() 时,
时,
点![]() 落在
落在![]() 上,
上,
由旋转可知![]()
![]()
过点![]() 作
作![]() ,垂足为
,垂足为![]()
则![]()
则![]()
![]() 点
点![]()
![]()
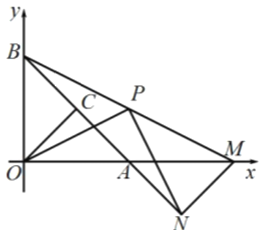
![]() 如图,当
如图,当![]() 时,
时,
点![]() 共线,点
共线,点![]() 共线
共线
![]() ,
,
且![]() 是
是![]() 中点,
中点,
![]() ,
,
且![]()
![]()
则![]()
可得![]()
![]()
即![]()
![]()
![]()
![]()
即![]()
![]() 当点B、M、N共线,M位于B、N之间时,如图
当点B、M、N共线,M位于B、N之间时,如图
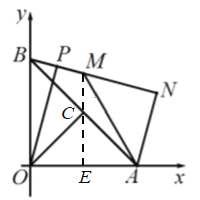
过M做![]() 于点E
于点E
由已知,![]() ,
,![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
则点M坐标为![]()
当点B、M、N共线,N位于B、M之间时,如图
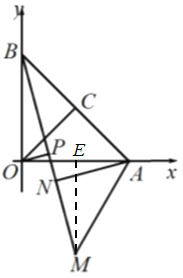
过M做![]() 于点E
于点E
由已知,![]() ,
,![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
则点M坐标为![]()
综上,点![]() 或
或![]()

练习册系列答案
相关题目