题目内容
13.若抛物线y=x2-2x+m与x轴的一个交点是(-2,0),则另一交点坐标是(4,0).分析 把(-2,0)代入抛物线y=x2-2x+m求出m的值,再令y=0,求出x的值即可.
解答 解:∵抛物线y=x2-2x+m与x轴的一个交点是(-2,0),
∴4+4+m=0,解得m=-8,
∴抛物线的解析式为y=x2-2x+8,
∴令y=0,则x2-2x+8=0,解得x1=-2,x2=4,
∴另一交点坐标是(4,0).
故答案为:(4,0).
点评 本题考查的是抛物线与x轴的交点,熟知x轴上点的坐标特点是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.某校2016年给希望工程捐款2万,以后每年都捐款,计划到2018年三年总共捐款6.62万元.若设该校捐款的年平均增长率为x,则可列方程为( )
| A. | 2+2×2(1+x)=6.62 | B. | 2(1+x)2=6.62 | ||
| C. | 2+2(1+x)+2(1+x)2=6.62 | D. | 2(1+x)(1+2x)=6.62 |
2.绝对值小于3的所有整数的和是( )
| A. | 3 | B. | 0 | C. | 6 | D. | -6 |
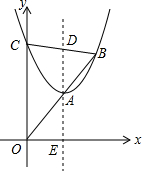 如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=$\frac{3}{2}$,直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是4.5或13.5.
如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=$\frac{3}{2}$,直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是4.5或13.5.