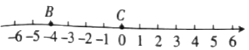题目内容
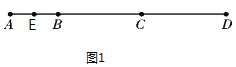
【题目】如图1,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 的路线以
的路线以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
![]()
(1)当![]() 时,则线段
时,则线段![]()
![]() ,线段
,线段![]()
![]() .
.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 的中点为
的中点为![]() ,问
,问![]() 的长是否变化?与点
的长是否变化?与点![]() 的位置是否无关?
的位置是否无关?
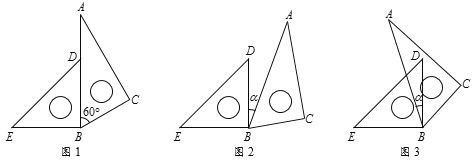
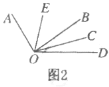
(4)知识迁移:如图2,已知![]() ,过角的内部任一点
,过角的内部任一点![]() 画射线
画射线![]() ,若
,若![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,问∠EOC的度数是否变化?与射线
,问∠EOC的度数是否变化?与射线![]() 的位置是否无关?
的位置是否无关?
【答案】(1)4,3;(2)![]() 或
或![]() ;(3)EC的长不变,与点B的位置无关,EC=5cm;(4)∠EOC的度数不变,与射线OB的位置无关.
;(3)EC的长不变,与点B的位置无关,EC=5cm;(4)∠EOC的度数不变,与射线OB的位置无关.
【解析】
(1)根据线段的和差关系可得;(2)分情况讨论:)①当0≤t≤5时,此时点B从A向D移动;②当5<t≤10时,此时点B从D向A移动;(3)根据线段中点定义可得:EC=EB+BC=![]() AB +
AB +![]() BD =
BD =![]() (AD+BD)=
(AD+BD)=![]() AD;(3)根据角平分线定义可得:∠EOC=∠EOB+∠BOC=
AD;(3)根据角平分线定义可得:∠EOC=∠EOB+∠BOC=![]() (∠AOB+∠BOD)=
(∠AOB+∠BOD)=![]() ∠AOD.
∠AOD.
解:(1)![]() 2×2=4(cm);
2×2=4(cm); ![]() =3(cm)
=3(cm)
![]()
(2)①当0≤t≤5时,此时点B从A向D移动:![]()
②当5<t≤10时,此时点B从D向A移动:![]()
(3)EC的长不变.与点B的位置无关.
∵AB中点为E,C是线段BD的中点,
∴EB=![]() AB,BC=
AB,BC=![]() BD.
BD.
∴EC=EB+BC=![]() AB +
AB +![]() BD =
BD =![]() (AD+BD)=
(AD+BD)=![]() AD
AD
∵AD=10 cm,
∴EC=5cm,与点B的位置无关.
(4)∠EOC的度数不变,与射线OB的位置无关.

∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠EOC=∠EOB+∠BOC
=![]() (∠AOB+∠BOD)
(∠AOB+∠BOD)
=![]() ∠AOD
∠AOD
∵∠AOD=120°
∴∠EOC=60°,与OB位置无关.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
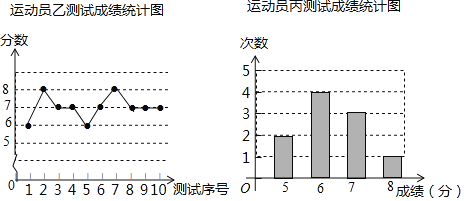
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?