题目内容
 如图,点A,B,C在⊙O上,∠AOC=80°,则∠ABC的度数为
如图,点A,B,C在⊙O上,∠AOC=80°,则∠ABC的度数为
- A.100°
- B.120°
- C.140°
- D.160°
C
分析:方法一:连接OB,根据等腰三角形的性质求出∠1+∠4=∠2+∠3=∠ABC,然后根据三角形内角和定理列出等式整理得到方法二:2∠ABC+∠AOC=360°,故易求∠ABC的值.或先求出弧ABC所对的圆周角等于圆心角∠AOC的一半,再根据圆内接四边形对角互补即可求出.
解答: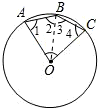 解:解法一:连接OB,则∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3=∠ABC,
解:解法一:连接OB,则∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3=∠ABC,
在△AOB中,∠1+∠2+∠AOB=180°----①;
在△OBC中,∠3+∠4+∠BOC=180°---②;
①+②得∠1+∠2+∠3+∠4+∠AOB+∠BOC=360°,∴2∠ABC+∠AOC=360°,
即∠ABC= (360°-80°)=140°.
(360°-80°)=140°.
故选C.
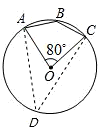
解法二:如图,作弧ABC所对的圆周角∠D,
∵∠AOC=80°,
∴∠D= ∠AOC=
∠AOC= ×80°=40°,
×80°=40°,
∴∠ABC=180°-∠D=140°.
故选C.
点评:解法一主要利用等腰三角形的性质及三角形内角和定理,关键在于连接OB把四边形的问题转化为两个三角形解决.
解法二利用圆周角定理和圆内接四边形的性质,要求对定理和性质熟练掌握并灵活运用.
分析:方法一:连接OB,根据等腰三角形的性质求出∠1+∠4=∠2+∠3=∠ABC,然后根据三角形内角和定理列出等式整理得到方法二:2∠ABC+∠AOC=360°,故易求∠ABC的值.或先求出弧ABC所对的圆周角等于圆心角∠AOC的一半,再根据圆内接四边形对角互补即可求出.
解答:
 解:解法一:连接OB,则∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3=∠ABC,
解:解法一:连接OB,则∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3=∠ABC,在△AOB中,∠1+∠2+∠AOB=180°----①;
在△OBC中,∠3+∠4+∠BOC=180°---②;
①+②得∠1+∠2+∠3+∠4+∠AOB+∠BOC=360°,∴2∠ABC+∠AOC=360°,
即∠ABC=
 (360°-80°)=140°.
(360°-80°)=140°.故选C.

解法二:如图,作弧ABC所对的圆周角∠D,
∵∠AOC=80°,
∴∠D=
 ∠AOC=
∠AOC= ×80°=40°,
×80°=40°,∴∠ABC=180°-∠D=140°.
故选C.
点评:解法一主要利用等腰三角形的性质及三角形内角和定理,关键在于连接OB把四边形的问题转化为两个三角形解决.
解法二利用圆周角定理和圆内接四边形的性质,要求对定理和性质熟练掌握并灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
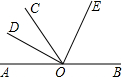 如图,点A,O,B在同一直线上,射线OD平分∠AOC,射线OE平分∠BOC.
如图,点A,O,B在同一直线上,射线OD平分∠AOC,射线OE平分∠BOC. 如图,点A、B、C在⊙O上,AO∥BC,∠OBC=40°,则∠ACB的度数是
如图,点A、B、C在⊙O上,AO∥BC,∠OBC=40°,则∠ACB的度数是 (2012•北京)已知:如图,点E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD.
(2012•北京)已知:如图,点E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD. (2012•鞍山)如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP.
(2012•鞍山)如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP. (2013•南通二模)如图,点A是双曲线y=
(2013•南通二模)如图,点A是双曲线y=