题目内容
一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销 售量可增加2万件.
售量可增加2万件.
⑴ 求出月销售量y(万件)与销售单价x(元)之间的函数关系式;
⑵ 求出月销售利润z(万元)与销售单价x(元)之间的函数关系式,并在下面坐标系中,画出图象草图;

⑶ 为了使月销售利润不低于480万元,请借助⑵中所画图象进行分析,说明销售单价的取值范围.
解:⑴  .
.
--  与
与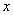 的函数关系式为
的函数关系式为 .
.
⑵  .
.
--  与
与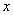 的函数关系式为
的函数关系式为 .
.
-- 草 图:
图:
⑶ 令 ,得
,得 ,整理得
,整理得 ,
,
-- 解得 ,
, .由图象可知,要使月销售利润不低于
.由图象可知,要使月销售利润不低于 万元,产品的销售单价应在
万元,产品的销售单价应在
 元到
元到 元之间(即
元之间(即 ).
).

练习册系列答案
相关题目
为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°.
体育成绩统计表
| 体育成绩(分) | 人数(人) |
|
| 26 | 8 | 16 |
| 27 | 24 | |
| 28 | 15 | |
| 29 |
| |
| 30 |
根据上面提供的信息,回答下列问题:
⑴ 填写表格中所缺数据,并写出样本容量与这些学生体育成绩的中位数;
⑵ 已知该校九年级共有500名学生,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的人数.
 x+b与反比例函数y=
x+b与反比例函数y= 中,x与y的对应值
中,x与y的对应值
 B.
B. C.
C. D.
D.
 、
、 分别切⊙
分别切⊙ 于点
于点 、
、 ,点
,点 是⊙
是⊙ ,则
,则 度;若PA=4,则AO= .
度;若PA=4,则AO= .

 百分比(%)
百分比(%) ,乙把ax-by=7看成ax-by=1,求得一个解为
,乙把ax-by=7看成ax-by=1,求得一个解为 ,则a,b的值分别为( )
,则a,b的值分别为( ) B、
B、 C、
C、 D、
D、
 、
、 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所