题目内容
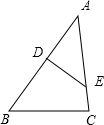D、E分别在△ABC的边AB、AC上，要使△AED∽△ABC，添加一个条件________（只能填一个）即可．
∠AED=∠B
分析：根据∠AEB=∠B和∠A=∠A可以求证△AED∽△ABC，故添加条件∠AEB=∠B即可以求证△AED∽△ABC．
解答：∵∠AEB=∠B，∠A=∠A，
∴△AED∽△ABC，
故添加条件∠AEB=∠B即可以使得△AED∽△ABC，
故答案为：∠AEB=∠B．
点评：本题考查了相似三角形的判定，等边三角形对应角相等的性质，本题中添加条件∠AEB=∠B并求证△AED∽△ABC是解题的关键．
分析：根据∠AEB=∠B和∠A=∠A可以求证△AED∽△ABC，故添加条件∠AEB=∠B即可以求证△AED∽△ABC．
解答：∵∠AEB=∠B，∠A=∠A，
∴△AED∽△ABC，
故添加条件∠AEB=∠B即可以使得△AED∽△ABC，
故答案为：∠AEB=∠B．
点评：本题考查了相似三角形的判定，等边三角形对应角相等的性质，本题中添加条件∠AEB=∠B并求证△AED∽△ABC是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
11、如图，D，E两点分别在△ABC的边AB，AC上，DE，BC不平行，若使△ADE∽△ABC，需要添加的条件是
如图，点D、E 分别在△ABC的边AB和AC上，且DE∥BC，∠1=∠2．问：△ABC是等腰三角形吗？请说明理由．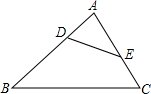
如图，D、E两点分别在△ABC的边AB、AC上，DE与BC不平行．