题目内容
一根横截面为圆形的下水管的直径为1米,管内污水的水面宽为0.8米,那么管内污水深度为________米.
0.2或0.8
分析:分为两种情况,画出图形,先连接OA,过O作OC⊥AB于点D,由垂径定理可知AD= AB,再在Rt△OAD中利用勾股定理可求出OD的长,再根据CD=OC-OD或CD=OC+OD即可得出结论.
AB,再在Rt△OAD中利用勾股定理可求出OD的长,再根据CD=OC-OD或CD=OC+OD即可得出结论.
解答: 解:分为两种情况:①如图所示:连接OA,过O作OC⊥AB于点D,
解:分为两种情况:①如图所示:连接OA,过O作OC⊥AB于点D,
∵OC⊥AB,AB=0.8米.
∴AD= AB=
AB= ×0.8=0.4米,
×0.8=0.4米,
∵圆形污水管道的直径为1米,
∴OA=OC=0.5米,
在Rt△OAD中,OD= =
= =0.3(米),
=0.3(米),
∴CD=OC-OD=0.5-0.3=0.2(米).
②如图CD=0.5+0.3=0.8(米)
故答案为:0.2或0.8.
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
分析:分为两种情况,画出图形,先连接OA,过O作OC⊥AB于点D,由垂径定理可知AD=
 AB,再在Rt△OAD中利用勾股定理可求出OD的长,再根据CD=OC-OD或CD=OC+OD即可得出结论.
AB,再在Rt△OAD中利用勾股定理可求出OD的长,再根据CD=OC-OD或CD=OC+OD即可得出结论.解答:
 解:分为两种情况:①如图所示:连接OA,过O作OC⊥AB于点D,
解:分为两种情况:①如图所示:连接OA,过O作OC⊥AB于点D,∵OC⊥AB,AB=0.8米.
∴AD=
 AB=
AB= ×0.8=0.4米,
×0.8=0.4米,∵圆形污水管道的直径为1米,
∴OA=OC=0.5米,
在Rt△OAD中,OD=
 =
= =0.3(米),
=0.3(米),∴CD=OC-OD=0.5-0.3=0.2(米).
②如图CD=0.5+0.3=0.8(米)

故答案为:0.2或0.8.
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
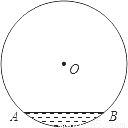
 一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.
一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.