题目内容
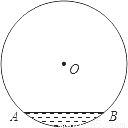
 一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.
一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.(1)求此时的水深(即阴影部分的弓形高);
(2)当水位上升到水面宽为0.8米时,求水面上升的高度.
分析:作半径OC⊥AB,连接OA,则CD即为弓形高.根据垂径定理的AD=
AB,然后根据已知条件求出CD的长;当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P,由此可得OP=0.3,然后根据MN与AB在圆心同侧或异侧时两种情况解答.
| 1 |
| 2 |
解答: 解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高
解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高
∵OC⊥AB,
∴AD=
AB
∵AO=0.5,AB=0.6,
∴AD=
AB=
×0.6=0.3,
∴OD=
=
=0.4,
∴CD=OC-OD=0.5-0.4=0.1米,即此时的水深为0.1米
(2)当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P
同理可得OP=0.3,
当MN与AB在圆心同侧时,水面上升的高度为0.1米;
当MN与AB在圆心异侧时,水面上升的高度为0.7米.
 解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高
解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高∵OC⊥AB,
∴AD=
| 1 |
| 2 |
∵AO=0.5,AB=0.6,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴OD=
| AO2-AD2 |
| 0.52-0.32 |
∴CD=OC-OD=0.5-0.4=0.1米,即此时的水深为0.1米
(2)当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P
同理可得OP=0.3,
当MN与AB在圆心同侧时,水面上升的高度为0.1米;
当MN与AB在圆心异侧时,水面上升的高度为0.7米.
点评:本题考查垂弦定理、圆心角、圆周角的应用能力.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目