题目内容
某商场将每件进价为60元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加20件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,商场一天可获利润y元.
①若商场经营该商品一天要获利润7000元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,并通过画该函数图象的草图,观察其图象的变化趋势,结合题意写出当x取何值时,商场获利润不少于7000元.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,商场一天可获利润y元.
①若商场经营该商品一天要获利润7000元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,并通过画该函数图象的草图,观察其图象的变化趋势,结合题意写出当x取何值时,商场获利润不少于7000元.
分析:(1)原来不降价时,利润=不降价时商品的单件利润×商品的件数;
(2)①先根据降价后的单件利润×降价后销售的商品的件数=7000,列出方程,再解方程求出未知数的值,进而得出每件商品应降价的钱数;
②根据利润=降价后的单件利润×降价后的销售量表示出函数关系式,然后画图回答问题即可.
(2)①先根据降价后的单件利润×降价后销售的商品的件数=7000,列出方程,再解方程求出未知数的值,进而得出每件商品应降价的钱数;
②根据利润=降价后的单件利润×降价后的销售量表示出函数关系式,然后画图回答问题即可.
解答:解:(1)若商店经营该商品不降价,则一天可获利润100×(100-60)=4000(元).
答:商场经营该商品原来一天可获利润4000元;
 (2)①依题意得:(100-60-x)(100+20x)=7000,
(2)①依题意得:(100-60-x)(100+20x)=7000,
即x2-35x+150=0,
解得:x1=5,x2=30.
经检验:x1=5,x2=30都是方程的解,且符合题意.
答:若商场经营该商品一天要获利润7000元,则每件商品应降价5元或30元;
②依题意得:y=(100-60-x)(100+20x),
即y=-20x2+700x+4000=-20(x-17.5)2+10125.
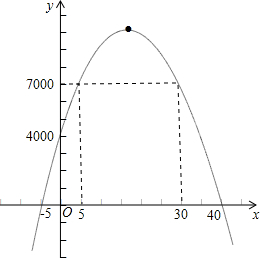
该函数图象的草图如右图所示:
观察图象可得:当5≤x≤30时,y≥7000,
故当5≤x≤30时,商店所获利润不少于7000元.
答:商场经营该商品原来一天可获利润4000元;
 (2)①依题意得:(100-60-x)(100+20x)=7000,
(2)①依题意得:(100-60-x)(100+20x)=7000,即x2-35x+150=0,
解得:x1=5,x2=30.
经检验:x1=5,x2=30都是方程的解,且符合题意.
答:若商场经营该商品一天要获利润7000元,则每件商品应降价5元或30元;
②依题意得:y=(100-60-x)(100+20x),
即y=-20x2+700x+4000=-20(x-17.5)2+10125.
该函数图象的草图如右图所示:
观察图象可得:当5≤x≤30时,y≥7000,
故当5≤x≤30时,商店所获利润不少于7000元.
点评:本题考查了二次函数在实际生活中的应用,难度中等.注意单件利润×销售的商品的件数=总利润.本题关键是求出利润的表达式,体现了函数与方程、不等式的关系.

练习册系列答案
相关题目