题目内容
 如图所示,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且∠PBC=∠C.
如图所示,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且∠PBC=∠C.(1)求证:CB∥PD;
(2)若BC等于3,sinP=
| 3 |
| 5 |
(3)连接OC,取其中点M,连接AM并延长交
 |
| BC |
分析:(1)根据圆周角定理得到∠D=∠PBC,而∠PBC=∠C,则∠D=∠C,然后根据平行线的判定定理即可得到结论;
(2)连AC,根据垂径定理及圆周角定理得到∠P=∠A,∠ACB=90°,则sinA=sinP=
,然后根据正弦的定义得到
=
,而BC=3,易得AB=5;
(3)连接BD,DF交BC于点N,由直径AB⊥CD,根据垂径定理得弧BC=弧BD,弧AC=弧AD,则BC=BD,∠ABC=∠ABD,根据圆周角定理有∠AOC=2∠ABC,则∠AOC=∠DBC,又∠A=∠BDF,根据相似三角形的判定可得△AOM∽△DNB,则OA:BD=OM:BN,即BD:BN=OA:OM,而点M为OC的中点,则OA=2OM,于是有BD=2BN,即可得到BC=2BN,BN=CN,即DF平分弦BC.
(2)连AC,根据垂径定理及圆周角定理得到∠P=∠A,∠ACB=90°,则sinA=sinP=
| 3 |
| 5 |
| BC |
| AB |
| 3 |
| 5 |
(3)连接BD,DF交BC于点N,由直径AB⊥CD,根据垂径定理得弧BC=弧BD,弧AC=弧AD,则BC=BD,∠ABC=∠ABD,根据圆周角定理有∠AOC=2∠ABC,则∠AOC=∠DBC,又∠A=∠BDF,根据相似三角形的判定可得△AOM∽△DNB,则OA:BD=OM:BN,即BD:BN=OA:OM,而点M为OC的中点,则OA=2OM,于是有BD=2BN,即可得到BC=2BN,BN=CN,即DF平分弦BC.
解答:(1)证明:∵∠D=∠PBC,∠PBC=∠C,
∴∠D=∠C,
∴CB∥PD;
(2)解:连接AC,如图,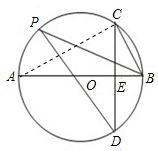
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴
=
,
∴∠P=∠A,
∴sinA=sinP=
,
又∵AB为直径,
∴∠ACB=90°,
∴sinA=
=
,
而BC=3,
∴AB=5,
即⊙O的直径为5;
(3)连接BD,DF交BC于点N,如图,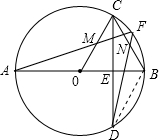
∵直径AB⊥CD,
∴弧BC=弧BD,弧AC=弧AD,
∴BC=BD,∠ABC=∠ABD,
∵∠AOC=2∠ABC,
∴∠AOC=∠DBC,
又∵∠A=∠BDF,
∴△AOM∽△DBN,
∴OA:BD=OM:BN,即BD:BN=OA:OM,
而点M为OC的中点,
∴OA=2OM,
∴BD=2BN,
∴BC=2BN,
∴BN=CN,即DF平分弦BC.
∴∠D=∠C,
∴CB∥PD;
(2)解:连接AC,如图,

∵AB是⊙O的直径,弦CD⊥AB于点E,
∴
 |
| BC |
 |
| BD |
∴∠P=∠A,
∴sinA=sinP=
| 3 |
| 5 |
又∵AB为直径,
∴∠ACB=90°,
∴sinA=
| BC |
| AB |
| 3 |
| 5 |
而BC=3,
∴AB=5,
即⊙O的直径为5;
(3)连接BD,DF交BC于点N,如图,

∵直径AB⊥CD,
∴弧BC=弧BD,弧AC=弧AD,
∴BC=BD,∠ABC=∠ABD,
∵∠AOC=2∠ABC,
∴∠AOC=∠DBC,
又∵∠A=∠BDF,
∴△AOM∽△DBN,
∴OA:BD=OM:BN,即BD:BN=OA:OM,
而点M为OC的中点,
∴OA=2OM,
∴BD=2BN,
∴BC=2BN,
∴BN=CN,即DF平分弦BC.
点评:本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧;运用相似三角形的判定与性质证明线段之间的关系;运用正弦的定义进行几何计算.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
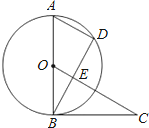 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.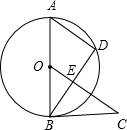 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.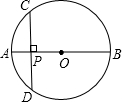 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为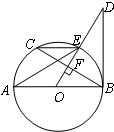 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )
如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )