题目内容
 如图,折叠的一边AD,使点D落在BC边的点F处,AE为折痕.
如图,折叠的一边AD,使点D落在BC边的点F处,AE为折痕.(1)求证:△AFB∽△FEC;
(2)若折痕AE=5
| 5 |
| 3 |
| 4 |
分析:(1)由四边形BCD是矩形,可得∠AFE=∠D=90°,又由同角的余角相等,可得∠BAF=∠EFC,即可证得:△AFB∽△FEC;
(2)由Rt△FEC中,tan∠EFC=
,可求得
=
,则可设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.继而求得BF与BC,则可求得k的值,由矩形ABCD的周长=2(AB+BC)求得结果.
(2)由Rt△FEC中,tan∠EFC=
| 3 |
| 4 |
| CE |
| CF |
| 3 |
| 4 |
解答:(1)证明:∵∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°,
又∵∠AFB+∠BAF=90°,
∴∠BAF=∠EFC,
又∠B=∠C=90°,
∴△AFB∽△FEC;
(2)Rt△FEC中,tan∠EFC=
,
∴
=
,
设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.
∴DC=8k,
又∵ABCD是矩形,
∴AB=8k,
Rt△AFB中,∠BAF=∠EFC,
∵tan∠BAF=
=
,
∴BF=6k,BC=10k
在Rt△AFE中由勾股定理得AE=5
k,又AE=5
,
∴k=1,
∴矩形ABCD的周长=2(AB+BC)=2(8k+10k)=36.
∴∠AFB+∠EFC=90°,
又∵∠AFB+∠BAF=90°,
∴∠BAF=∠EFC,
又∠B=∠C=90°,
∴△AFB∽△FEC;
(2)Rt△FEC中,tan∠EFC=
| 3 |
| 4 |
∴
| CE |
| CF |
| 3 |
| 4 |
设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.
∴DC=8k,
又∵ABCD是矩形,
∴AB=8k,
Rt△AFB中,∠BAF=∠EFC,
∵tan∠BAF=
| 3 |
| 4 |
| BF |
| AB |
∴BF=6k,BC=10k
在Rt△AFE中由勾股定理得AE=5
| 5 |
| 5 |
∴k=1,
∴矩形ABCD的周长=2(AB+BC)=2(8k+10k)=36.
点评:此题考查了相似三角形的判定与性质、矩形的性质、折叠的性质以及勾股定理等知识.此题综合性很强,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
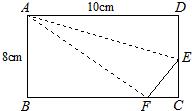 15、如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求:(1)FC的长;(2)EF的长.
15、如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求:(1)FC的长;(2)EF的长.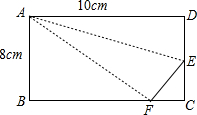 如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求EC的长.
如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求EC的长. 如图,折叠的一边AD,使点D落在BC边的点F处,AE为折痕.
如图,折叠的一边AD,使点D落在BC边的点F处,AE为折痕.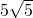 ,且tan∠EFC=
,且tan∠EFC= ,求矩形ABCD的周长.
,求矩形ABCD的周长. ,且tan∠EFC=
,且tan∠EFC= ,求矩形ABCD的周长.
,求矩形ABCD的周长.