题目内容
（1）如图1，已知直线m平行于直线n，折线ABC是夹在m与n之间的一条折线，则∠1、∠2、∠3的度数之间有什么关系？为什么？
（2）如图2，直线m依然平行于直线n，则此时∠1、∠2、∠3、∠4之间有什么关系？（只需写出结果）
（2）如图2，直线m依然平行于直线n，则此时∠1、∠2、∠3、∠4之间有什么关系？（只需写出结果）
分析：（1）过点B作DE∥m，根据平行线的性质：两直线平行，内错角相等即可得到结论．
（2）过点B作BE∥m，过点C作CF∥m，根据平行线的性质：两直线平行，内错角相等即可得到结论．
（2）过点B作BE∥m，过点C作CF∥m，根据平行线的性质：两直线平行，内错角相等即可得到结论．
解答：
解：过点B作DE∥m．（1分）
因为DE∥m（已知），
所以∠1=∠ABE（两直线平行，内错角相等）．（1分）
因为m∥n，且DE∥m（已知），
所以DE∥n（平行于同一条直线的两条直线互相平行），（2分）
所以∠3=∠EBC（两直线平行，内错角相等），（1分）
因为∠2=∠ABE+∠EBC，
所以∠2=∠1+∠3（等量代换）；（1分）
（2）∠1+∠3=∠2+∠4．（2分）
解：过点B作DE∥m．（1分）因为DE∥m（已知），
所以∠1=∠ABE（两直线平行，内错角相等）．（1分）
因为m∥n，且DE∥m（已知），
所以DE∥n（平行于同一条直线的两条直线互相平行），（2分）
所以∠3=∠EBC（两直线平行，内错角相等），（1分）
因为∠2=∠ABE+∠EBC，
所以∠2=∠1+∠3（等量代换）；（1分）
（2）∠1+∠3=∠2+∠4．（2分）点评：本题主要考查了平行线的性质：两直线平行，内错角相等．正确作辅助线是解题关键．（2）中将∠2、∠3拆分是解题的关键．
练习册系列答案
53随堂测系列答案
相关题目
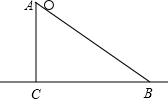在地面上有一个斜坡装置（如图），已知斜坡的铅直高度AC=0.6m，水平距离BC=0.8m，小球从顶端A由静止自由下滑，速度均匀增大，0.2s滑至底端B后，继续在平地上滑行15米停止．
