题目内容
 如图,过P点作3条线段MN,IJ,EF分别平行于△ABC的三边,把△ABC分成三个三角形和三个平行四边形,图中标出了其中三个的面积:S△IMP=9,S□BFPM=42,S?CNPJ=70,则S△ABC=________.
如图,过P点作3条线段MN,IJ,EF分别平行于△ABC的三边,把△ABC分成三个三角形和三个平行四边形,图中标出了其中三个的面积:S△IMP=9,S□BFPM=42,S?CNPJ=70,则S△ABC=________.
225
分析:根据△IMP和平行四边形MBFP的面积得到IM:MB的值,然后用相似三角形的面积的比等于相似比的平方,求出△PFJ的面积,由△PFJ和平行四边形MBFP以及平行四边形PJCN的面积得到FJ:BC的值,再求出△ABC的面积.
解答: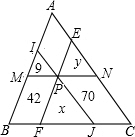 解:如图,设S△PFJ=x,则因△IMP∽△PFJ∽△IBJ,相似比为IM:PF:IB,面积比为IM2:PF2:IB2,
解:如图,设S△PFJ=x,则因△IMP∽△PFJ∽△IBJ,相似比为IM:PF:IB,面积比为IM2:PF2:IB2,
∵S△IMP=9,SBFPM=42,
∴IM:MB=3:7,IM:IB=3:10.
∴S△IMP:S△IBJ=9:100=9:(9+42+x),
得:x=49.
∵S△PFJ=49,SCNPJ=70,
∴FJ:JC=7:5,FJ:FC=7:12,
∴S△PFJ:S△EFC=49:144=49:(49+70+y)
得:y=25.
由四边形MBFP,三角形PFJ,四边形PJCN的面积可以得到:BF:FJ:JC=3:7:5,
∴FJ:BC=7:15.
∵△PFJ∽△ABC,
∴S△PFJ:S△ABC=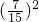 =
=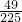 ,
,
而S△PFJ=49,∴S△ABC=225.
故答案是:225.
点评:本题考查的是相似三角形的判定与性质,根据平行判定三角形相似,运用相似三角形面积的比等于相似比的平方进行计算求出△ABC的面积.
分析:根据△IMP和平行四边形MBFP的面积得到IM:MB的值,然后用相似三角形的面积的比等于相似比的平方,求出△PFJ的面积,由△PFJ和平行四边形MBFP以及平行四边形PJCN的面积得到FJ:BC的值,再求出△ABC的面积.
解答:
 解:如图,设S△PFJ=x,则因△IMP∽△PFJ∽△IBJ,相似比为IM:PF:IB,面积比为IM2:PF2:IB2,
解:如图,设S△PFJ=x,则因△IMP∽△PFJ∽△IBJ,相似比为IM:PF:IB,面积比为IM2:PF2:IB2,∵S△IMP=9,SBFPM=42,
∴IM:MB=3:7,IM:IB=3:10.
∴S△IMP:S△IBJ=9:100=9:(9+42+x),
得:x=49.
∵S△PFJ=49,SCNPJ=70,
∴FJ:JC=7:5,FJ:FC=7:12,
∴S△PFJ:S△EFC=49:144=49:(49+70+y)
得:y=25.
由四边形MBFP,三角形PFJ,四边形PJCN的面积可以得到:BF:FJ:JC=3:7:5,
∴FJ:BC=7:15.
∵△PFJ∽△ABC,
∴S△PFJ:S△ABC=
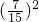 =
=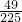 ,
,而S△PFJ=49,∴S△ABC=225.
故答案是:225.
点评:本题考查的是相似三角形的判定与性质,根据平行判定三角形相似,运用相似三角形面积的比等于相似比的平方进行计算求出△ABC的面积.

练习册系列答案
相关题目



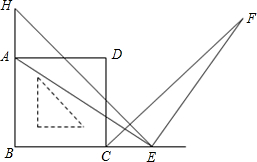 重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由.
重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由.