Question

如图，一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边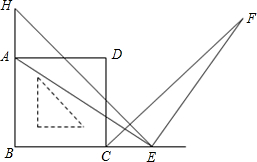重合，过E点作EF⊥AE交∠DCE的角平分线于F点，试探究线段AE与EF的数量关系，并说明理由．
（1）求证：∠DAE=∠BEA；
（2）探究线段AE与EF的数量关系，并说明理由．

Answer 1

分析：（1）根据正方形的性质得出AD∥BE，根据平行线的性质即可得到答案；
（2）AE=EF．根据正方形的性质推出AB=BC，∠BAD=∠HAD=∠DCE=90°，推出∠HAE=∠CEF，根据△HEB是以∠B为直角的等腰直角三角形，得到BH=BE，∠H=45°，HA=EC，根据CF平分∠DCE推出∠AHE=∠FCE，根据ASA证△HAE≌△CEF即可得到答案．

解答：（1）证明：∵四边形ABCD是正方形，
∴AD∥BE，
∴∠DAE=∠BEA；

（2）答：AE=EF．
理由如下：
∵四边形ABCD是正方形，
∴AB=BC，∠BAD=∠HAD=∠DCE=90°，
又∵EF⊥AE，
∴∠AEF=90°，
又∵∠DAE=∠BEA（已证），
∴∠HAE=∠HAD+∠DAE=∠AEF+∠BEA=∠CEF，
又∵△HEB是以∠B为直角的等腰直角三角形，
∴BH=BE，∠H=45°，HA=BH-BA=BE-BC=EC，
又∵CF平分∠DCE，
∴∠FCE=

1

2

×90°=45°=∠EHA，
在△HAE和△CEF中

∠EHA=∠FCE AH=EC ∠HAE=∠CEF

∴△HAE≌△CEF（ASA），
∴AE=EF．

点评：本题主要考查对正方形的性质，平行线的性质和判定，角平分线的性质，等腰三角形的性质，全等三角形的性质和判定等知识点的理解和掌握，能综合运用这些性质进行推理是证此题的关键，题型较好，综合性强．