题目内容
如图,将含有30°的两个全等的直角三角形△ABD与△AMF如图拼在一起,将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K,设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,旋转角β的度数为 .
【答案】分析:根据旋转的性质得∠DAD1=β,而△AFK为等腰三角形,讨论:当KA=KF,则∠KAF=∠F=30°,通过互余即可得到β;当FK=FA,∠FAK=∠FKA= (180°-30°)=75°,通过互余即可得到β.
(180°-30°)=75°,通过互余即可得到β.
解答:解:∵△ABD绕点A顺时针旋转得△AB1D1,
∴∠DAD1=β,
∵△AFK为等腰三角形,
①当KA=KF,
∴∠KAF=∠F=30°,
∴β=∠DAD1=90°-30°=60°;
②当FK=FA,
∴∠FAK=∠FKA= (180°-30°)=75°,
(180°-30°)=75°,
∴β=∠DAD1=90°-75°=15°.
故答案为60°或15°.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应线段相等,对应角相等.也考查了等腰三角形的性质.
 (180°-30°)=75°,通过互余即可得到β.
(180°-30°)=75°,通过互余即可得到β.解答:解:∵△ABD绕点A顺时针旋转得△AB1D1,
∴∠DAD1=β,
∵△AFK为等腰三角形,
①当KA=KF,
∴∠KAF=∠F=30°,
∴β=∠DAD1=90°-30°=60°;
②当FK=FA,
∴∠FAK=∠FKA=
 (180°-30°)=75°,
(180°-30°)=75°,∴β=∠DAD1=90°-75°=15°.
故答案为60°或15°.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应线段相等,对应角相等.也考查了等腰三角形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,将含有30°角的三角尺ABC绕点B旋转到△DBE的位置,当C、B、E在同一条直线上时,∠BDC等于
如图,将含有30°角的三角尺ABC绕点B旋转到△DBE的位置,当C、B、E在同一条直线上时,∠BDC等于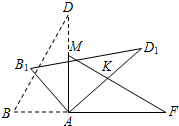 如图,将含有30°的两个全等的直角三角形△ABD与△AMF如图拼在一起,将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K,设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,旋转角β的度数为
如图,将含有30°的两个全等的直角三角形△ABD与△AMF如图拼在一起,将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K,设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,旋转角β的度数为
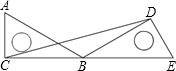 如图,将含有30°角的三角尺ABC绕点B旋转到△DBE的位置,当C、B、E在同一条直线上时,∠BDC等于________度.
如图,将含有30°角的三角尺ABC绕点B旋转到△DBE的位置,当C、B、E在同一条直线上时,∠BDC等于________度.