题目内容
 如图,将含有30°角的三角尺ABC绕点B旋转到△DBE的位置,当C、B、E在同一条直线上时,∠BDC等于
如图,将含有30°角的三角尺ABC绕点B旋转到△DBE的位置,当C、B、E在同一条直线上时,∠BDC等于分析:由题意可知,△ACB≌△EDB,可得BC=BD,则∠BCD=∠BDC,又点C、B、E在同一条直线上,所以,可得∠CBD=150°,∠BDC=15°.
解答:解:如图,
∵含有30°角的三角尺ABC绕点B旋转到△DBE的位置,
∴△ACB≌△EDB,
∴BC=BD,即∠BCD=∠BDC,
又∵点C、B、E在同一条直线上,
∴∠CBD=150°,
∴∠BDC=
=15°.
故答案为:15.
∵含有30°角的三角尺ABC绕点B旋转到△DBE的位置,
∴△ACB≌△EDB,
∴BC=BD,即∠BCD=∠BDC,
又∵点C、B、E在同一条直线上,
∴∠CBD=150°,
∴∠BDC=
| 180°-150° |
| 2 |
故答案为:15.
点评:本题主要考查了旋转的性质、等腰三角形的性质,掌握旋转前后的两个三角形全等是解答本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
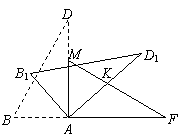
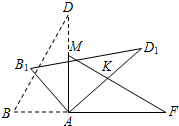 如图,将含有30°的两个全等的直角三角形△ABD与△AMF如图拼在一起,将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K,设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,旋转角β的度数为
如图,将含有30°的两个全等的直角三角形△ABD与△AMF如图拼在一起,将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K,设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,旋转角β的度数为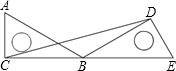 如图,将含有30°角的三角尺ABC绕点B旋转到△DBE的位置,当C、B、E在同一条直线上时,∠BDC等于________度.
如图,将含有30°角的三角尺ABC绕点B旋转到△DBE的位置,当C、B、E在同一条直线上时,∠BDC等于________度.