题目内容
如图，已知四边形ABDC中，AB=AC，对角线AD和BC相交于点E，∠BDA=∠ACB．求证：AB2=AE•AD．
证明：∵AB=AC，
∴∠ABC=∠ACB，
∵∠ADB=∠ACB
∴∠ADB=∠ABC，
∵∠BAE=∠BAD，
∴△ABE∽△ADB，
∴
，
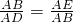∴AB2=AD•AE．
分析：本题只需根据题意条件判断出∠ABC=∠ACB、∠ADB=∠ABC，然后结合题意可判断出△ABE∽△ADB，从而利用相似三角形的性质可得出结论．
点评：本题考查相似三角形的性质，难度一般，解答本题的关键是根据题意确定结论涉及的线段所在的三角形，然后利用相似的知识进行求解．
∴∠ABC=∠ACB，
∵∠ADB=∠ACB
∴∠ADB=∠ABC，
∵∠BAE=∠BAD，
∴△ABE∽△ADB，
∴
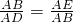，∴AB2=AD•AE．
分析：本题只需根据题意条件判断出∠ABC=∠ACB、∠ADB=∠ABC，然后结合题意可判断出△ABE∽△ADB，从而利用相似三角形的性质可得出结论．
点评：本题考查相似三角形的性质，难度一般，解答本题的关键是根据题意确定结论涉及的线段所在的三角形，然后利用相似的知识进行求解．
练习册系列答案
相关题目
15、如图，已知四边形ABCD是等腰梯形，AB=DC，AD∥BC，PB=PC．求证：PA=PD．
的延长线分别交于点F、E，且
（2013•梧州）如图，已知：AB∥CD，BE⊥AD，垂足为点E，CF⊥AD，垂足为点F，并且AE=DF．
≌
