题目内容
 如图,在等腰梯形ABCD中,AD∥BC,点E、F、G分别在边AB、BC、CD上,四边形AEFG是正方形,如果∠B=60°,AD=1,那么BC的长是
如图,在等腰梯形ABCD中,AD∥BC,点E、F、G分别在边AB、BC、CD上,四边形AEFG是正方形,如果∠B=60°,AD=1,那么BC的长是考点:等腰梯形的性质,等边三角形的判定与性质,正方形的性质
专题:
分析:过点D作DN⊥AG于点N,利用等腰梯形的性质以及正方形的性质得出AN以及AG的长,再利用锐角三角函数关系得出BF的长,再利用等边三角的判定得出FC的长,即可得出答案.
解答: 解:过点D作DN⊥AG于点N,
解:过点D作DN⊥AG于点N,
∵在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=1,
∴∠C=60°,∠BAD=120°,∠ADC=120°,
∵四边形AEFG是正方形,
∴∠BAG=90°,
∴∠DAG=30°,
∴∠DGA=30°,
∵DN⊥AG,∴AN=NG,
∴AD=DG=1,DN=
AD=
,
∴AN=
,
∴AG=AE=EF=FG=
,
∴BF=
=
=2,
∵∠FGA=90°,∠AGD=30°,
∴∠FGC=60°,
又∵∠C=60°,
∴△FGC是等边三角形,
∴FC=FG=
,
∴BC=BF+FC=2+
.
故答案为:2+
.
 解:过点D作DN⊥AG于点N,
解:过点D作DN⊥AG于点N,∵在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=1,
∴∠C=60°,∠BAD=120°,∠ADC=120°,
∵四边形AEFG是正方形,
∴∠BAG=90°,
∴∠DAG=30°,
∴∠DGA=30°,
∵DN⊥AG,∴AN=NG,
∴AD=DG=1,DN=
| 1 |
| 2 |
| 1 |
| 2 |
∴AN=
| ||
| 2 |
∴AG=AE=EF=FG=
| 3 |
∴BF=
| EF |
| sin60° |
| ||||
|
∵∠FGA=90°,∠AGD=30°,
∴∠FGC=60°,
又∵∠C=60°,
∴△FGC是等边三角形,
∴FC=FG=
| 3 |
∴BC=BF+FC=2+
| 3 |
故答案为:2+
| 3 |
点评:此题主要考查了等腰梯形的性质以及正方形的性质、勾股定理以及锐角三角函数关系等知识,得出EF的长是解题关键.

练习册系列答案
相关题目
x<0,y>0时,则x,y,0中最大的数是( )
| A、x | B、y | C、0 | D、没有 |
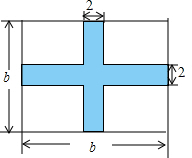 如图,在一块长为a米,宽为b米的长方形草地上,修建两条宽为2米的甬道.
如图,在一块长为a米,宽为b米的长方形草地上,修建两条宽为2米的甬道. 如图,⊙B的半径为4cm,∠MBN=60°,点A、C分别是射线BM、BN上的动点,且直线AC⊥BN.当AC平移到与⊙B相切时,AB的长度是
如图,⊙B的半径为4cm,∠MBN=60°,点A、C分别是射线BM、BN上的动点,且直线AC⊥BN.当AC平移到与⊙B相切时,AB的长度是