题目内容
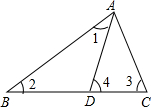
如图,在△ABC中,∠ABC的角平分线和外角∠ACD的角平分线相交于点E,如果已知∠A=60°,∠ABC=50°,求∠E的大小?


在△ABC中,∵∠A=60°,∠ABC=50°,
∴∠ACB=70°,
∴∠ACD=110°,
∵BE、CE平分∠ABC、∠ACD,
∴∠EBC=
∠ABC=25°,∠BCE=∠ACB+
∠ACD=70°+55°=125°,
∴在△BCE中,∠E=180°-∠EBC-∠ECB=180°-25°-125°=30°.
故∠E的大小为30°.
故答案为:30°.
∴∠ACB=70°,
∴∠ACD=110°,
∵BE、CE平分∠ABC、∠ACD,
∴∠EBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴在△BCE中,∠E=180°-∠EBC-∠ECB=180°-25°-125°=30°.
故∠E的大小为30°.
故答案为:30°.

练习册系列答案
相关题目