题目内容
 如图,AB是半圆的直径,AB=4,BC=3,∠ABC的平分线交半圆于D,AD、BC的延长线交于E,则四边形ABCD的面积是△DCE面积的________倍.
如图,AB是半圆的直径,AB=4,BC=3,∠ABC的平分线交半圆于D,AD、BC的延长线交于E,则四边形ABCD的面积是△DCE面积的________倍.
7
分析:连OC,AC,先由DB平分∠ABC,可得到OD∥BE,则OD为△ABC的中位线,OD= AB=
AB= ×4=2,EC=1,在Rt△ABC中,利用勾股定理可求得AC=
×4=2,EC=1,在Rt△ABC中,利用勾股定理可求得AC= =
= ,从而在Rt△ACE中,利用勾股定理得到AE=
,从而在Rt△ACE中,利用勾股定理得到AE= =2
=2 ,然后利用△EDC∽△EBA得到它们的面积比,最后得四边形ABCD的面积与△DCE面积的数量关系.
,然后利用△EDC∽△EBA得到它们的面积比,最后得四边形ABCD的面积与△DCE面积的数量关系.
解答: 解:连OC,AC,如图,
解:连OC,AC,如图,
∵DB平分∠ABC,
∴∠DBC=∠ABD,
而∠OBD=∠ODB,
∴∠ODB=∠DBC,
∴OD∥BE,
而O为AB的中点,
∴OD为△ABC的中位线,
∴OD= AB=
AB= ×4=2,
×4=2,
∴BE=4,则EC=4-3=1,
由AB是直径,所以∠ACB=90°,
∴AC= =
= ,
,
∴AE= =2
=2 ,
,
又∵∠EDC=∠ABE,
∴△EDC∽△EBA,
∴S△EDC:S△EBA=( )2=(
)2=(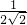 )2=
)2= ,
,
所以S△EDC:S四边形ABCD=1:7,
故答案为7.
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了圆周角的推论:直径所对的圆周角为90度,
分析:连OC,AC,先由DB平分∠ABC,可得到OD∥BE,则OD为△ABC的中位线,OD=
 AB=
AB= ×4=2,EC=1,在Rt△ABC中,利用勾股定理可求得AC=
×4=2,EC=1,在Rt△ABC中,利用勾股定理可求得AC= =
= ,从而在Rt△ACE中,利用勾股定理得到AE=
,从而在Rt△ACE中,利用勾股定理得到AE= =2
=2 ,然后利用△EDC∽△EBA得到它们的面积比,最后得四边形ABCD的面积与△DCE面积的数量关系.
,然后利用△EDC∽△EBA得到它们的面积比,最后得四边形ABCD的面积与△DCE面积的数量关系.解答:
 解:连OC,AC,如图,
解:连OC,AC,如图,∵DB平分∠ABC,
∴∠DBC=∠ABD,
而∠OBD=∠ODB,
∴∠ODB=∠DBC,
∴OD∥BE,
而O为AB的中点,
∴OD为△ABC的中位线,
∴OD=
 AB=
AB= ×4=2,
×4=2,∴BE=4,则EC=4-3=1,
由AB是直径,所以∠ACB=90°,
∴AC=
 =
= ,
,∴AE=
 =2
=2 ,
,又∵∠EDC=∠ABE,
∴△EDC∽△EBA,
∴S△EDC:S△EBA=(
 )2=(
)2=(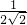 )2=
)2= ,
,所以S△EDC:S四边形ABCD=1:7,
故答案为7.
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了圆周角的推论:直径所对的圆周角为90度,

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)


