题目内容
分别以下列四组数为一个三角形的三边长:①1、2、3;②2、3、4;③3、4、5;④4、5、6; 其中能构成直角三角形的有( )
A.1 组 B.2 组 C.3 组 D.4 组
A【考点】勾股数.
【分析】欲判断是否能构成直角三角形,需验证两小边的平方和是否等于最长边的平方.
【解答】解:①12+22≠32,不能构成直角三角形;
②22+32≠42,不能构成直角三角形;
③32+42=52,能构成直角三角形;
④42+52≠62,不能构成直角三角形. 其中能构成直角三角形的只有 1 组. 故选:A.
【点评】此题主要考查了勾股定理的逆定理:已知△ABC 的三边满足 a2+b2=c2,则△ABC 是直角三 角形.

练习册系列答案
相关题目
观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
| 图① | 图② | 图③ | |
| 三个角上三个数的 积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 | (﹣2)×(﹣5)×17=170 |
| 三个角上三个数的 和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 | (﹣2)+(﹣5)+17 |
| 积与和的商 | (﹣2)÷2=﹣1 | (﹣60)÷(﹣12)=5 | 170÷10=17 |
请用你发现的规律求出图④中的数 x 和图⑤中的数 y.

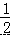
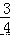 ×[4﹣(﹣2)3
×[4﹣(﹣2)3 =10
=10
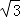 A.3 B.4 C.2
A.3 B.4 C.2 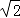 D.2
D.2