题目内容
如图，反比例函数
的图象与正比例函数
的图象交于点（2，1），则使y1＞y2的x的取值范围是【 】
的图象与正比例函数的图象交于点（2，1），则使y1＞y2的x的取值范围是【 】| A．0＜x＜2 | B．x＞2 | C．x＞2或-2＜x＜0 | D．x＜－2或0＜x＜2 |
D。
先根据反比例函数与正比例函数的性质求出B点坐标，由函数图象即可得出结论：
∵反比例函数与正比例函数的图象均关于原点对称，∴A、B两点关于原点对称。
∵A（2，1），∴B（－2，－1）。
∵由函数图象可知，当0＜x＜2或x＜－2时函数y1的图象在y2的上方，
∴使y1＞y2的x的取值范围是x＜－2或0＜x＜2。故选D。
∵反比例函数与正比例函数的图象均关于原点对称，∴A、B两点关于原点对称。
∵A（2，1），∴B（－2，－1）。
∵由函数图象可知，当0＜x＜2或x＜－2时函数y1的图象在y2的上方，
∴使y1＞y2的x的取值范围是x＜－2或0＜x＜2。故选D。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
和反比例函数
的图像，判断下列结论错误的有（ ）
＞
＞
＞0；
的解为
，
；
＞
.
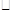OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数
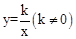的图像经过点B.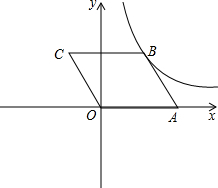
与反比例函数
的图象在第一象限的交点为
．
与
的值；
轴交于点
，连接
，求
的度数．
经过矩形OABC的边BC的中点E，交AB于点D.若梯形ODBC的面积为5，则双曲线的解析式为（）
B．
C．
D．
的图象上，若S△BCD=9，则k=___________.
与正比例函数
的图象的一个交点是
，若
，则
的取值范围在数轴上表示为（ ）
的图象在第二、四象限，则m的取值范围是
，斜边
,反比例函数
的图像经过AO的中点C，且与AB交于点D,则点D的坐标为 . 