Question

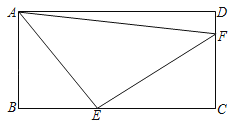
【题目】如图，在长方形ABCD中，点E在BC上，点F在CD上，且满足BE＝CF＝a，AB＝EC＝b．

（1）判断△AEF的形状，并证明你的结论；

（2）请用含a，b的代数式表示△AEF的面积；

（3）当△ABE的面积为24，BC长为14时，求△ADF的面积．

Answer 1

【答案】（1）△AEF是等腰直角三角形，理由详见解析；（2）（a2+b2）；（3）14．

【解析】

（1）证明△ABE≌△ECF（SAS），得出AE＝EF，∠BAE＝∠CEF，证出∠AEF＝90°，即可得出△AEF是等腰直角三角形；

（2）由勾股定理得出AE2＝AB2+BE2＝a2+b2，由三角形面积公式即可得出答案；

（3）求出ab＝48，由题意得出（a+b）2＝142，求出a2+b2＝100，得出（a﹣b）2＝4，证出b﹣a＝2，由三角形面积公式即可得出答案．

（1）△AEF是等腰直角三角形，理由如下：

∵四边形ABCD是矩形，

∴∠B＝∠D＝∠C＝90°，AD＝BC＝a+b，

在△ABE和△ECF中， ，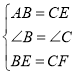

∴△ABE≌△ECF（SAS），

∴AE＝EF，∠BAE＝∠CEF，

∵∠BAE+∠AEB＝90°，

∴∠CEF+∠AEB＝90°，

∴∠AEF＝90°，

∴△AEF是等腰直角三角形；

（2）∵∠B＝90°，BE＝CF＝a，AB＝CE＝b，

∴AE2＝AB2+BE2＝a2+b2，

∴△AEF的面积＝AE×EF＝AE2＝（a2+b2）；

（3）∵△ABE的面积＝24＝ab，

∴ab＝48，

∵BC＝14，

∴a+b＝14，

∴（a+b）2＝142，

∴a2+2ab+b2＝196，

∴a2+b2＝100，

∴a2﹣2ab+b2＝100﹣96＝4，

即（a﹣b）2＝4，

∵CD＞F，

∴b＞a，

∴b﹣a＝2，

∴△ADF的面积＝AD×DF＝BC×（b﹣a）＝×14×2＝14．