题目内容
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中点,将
边上的中点,将![]() 绕点
绕点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() 得到
得到![]() ,
,![]() 的两边分别与
的两边分别与![]() 、
、![]() 边相交于点
边相交于点![]() ,
,![]() 两点,连结
两点,连结![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)当![]() 变成等腰直角三角形时,求
变成等腰直角三角形时,求![]() 的长;
的长;
(4)在此运动变化的过程中,四边形![]() 的面积是否保持不变?试说明理由.
的面积是否保持不变?试说明理由.

【答案】(1)证明见解析;(2)![]() ;(3)0或4;(4)不变,理由见解析.
;(3)0或4;(4)不变,理由见解析.
【解析】
(1)结合等腰三角形的性质和旋转的性质利用ASA可得![]() ;
;
(2)由全等三角形的性质可得![]() ,可知
,可知![]() ,可求度数;
,可求度数;
(3)考虑点E与点C重合和点![]() 到
到![]() 的中点的情况即可;
的中点的情况即可;
(4)根据![]() 计算即可.
计算即可.
(1)![]() 中
中![]()
![]()
![]() ,
,
![]() ,
,![]() 是
是![]() 边上的中点,
边上的中点,
![]() 也是顶角的角平分线,
也是顶角的角平分线,
也是底边![]() 边上的高线(等腰三角形三线合一)
边上的高线(等腰三角形三线合一)
![]()
![]()
![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
在![]() 和
和![]() 中
中
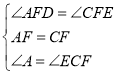
![]()
(2)![]() (已证)
(已证)
![]() (全等三角形对应边相等)
(全等三角形对应边相等)
![]()
![]()
(3)点![]() 与
与![]() 重合时,即
重合时,即![]() 时,
时,![]() 会成等腰直角三角形.
会成等腰直角三角形.
点![]() 到
到![]() 的中点时,即
的中点时,即![]() 时,
时,![]() 会成等腰直角三角形.
会成等腰直角三角形.
(4)在此运动变化的过程中,四边形![]() 的面积保持不变.
的面积保持不变.
理由如下:
![]()
![]()
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






