Question

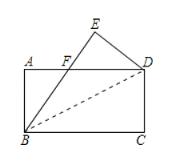
【题目】如图，将矩形()沿折叠后，点落在点处，且交于点，若，.

(1)求的长；

(2)求和的面积；

(3)求中点到边上的距离.

Answer 1

【答案】(1)DF=5；(2)S△DBF=10；S△DEF=6；(3).

【解析】

（1）易证BF=FD，在直角△ABF中，根据勾股定理就可以求出DF的长；
（2）由折叠的性质得BE=BC=8，DE=CD=4，∠E=90°，EF=BE-BF=3，由S△DEF= EFDE，S△DBF=S△BDE-S△DEF即可得出结果；
（3）由勾股定理得出BD= ，设F到BD边上的距离为h，则S△DBF= BDh，即可得出结果．

解：(1)∵四边形是矩形

∴，，，

∴

由折叠性质得：，

∴

∴

设，则

在中，由勾股定理得：

即：，解得：，

∴

(2)由折叠的性质得：，，，，

∴

(3)

设到边上的距离为

则，即：，解得：

∴到边上的距离为