题目内容
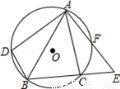
(本题满分12分)如图1,在平面直角坐标系中,点M在x轴的正半轴上,⊙M交x轴 于A、B两点,交y轴C、D于两点,且C为弧AE的中点,AE交y轴于点G,若A点的坐标为(-2,0),CD=8
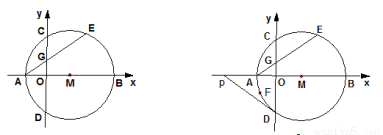
(1)求⊙M的半径
(2)求AE的长
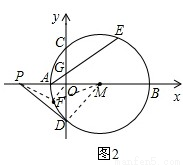
(3)如图2,过点D作⊙M的切线,交x轴于点P.动点F在⊙M圆周上运动时,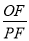 的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
见解析
【解析】
试题分析:(1)连结CM,则AB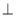 CD,所以OC=0D=4,设⊙M的半径为r,A点的坐标为(-2,0),所以OM=r-2,在Rt△OCM中,根据勾股定理可得r=5;(2)因为AB
CD,所以OC=0D=4,设⊙M的半径为r,A点的坐标为(-2,0),所以OM=r-2,在Rt△OCM中,根据勾股定理可得r=5;(2)因为AB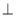 CD,所以弧AC=弧AD,又C为弧AE的中点,所以可证弧CD=弧AE,所以AE=CD=8;(3)连结AM,利用△MOD∽△MDP, △MOD∽△DOP可得OP=
CD,所以弧AC=弧AD,又C为弧AE的中点,所以可证弧CD=弧AE,所以AE=CD=8;(3)连结AM,利用△MOD∽△MDP, △MOD∽△DOP可得OP=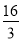 ,然后分三种情况讨论:点F与点A重合,点F与点B重合,点F与点A、B都不重合,可求出
,然后分三种情况讨论:点F与点A重合,点F与点B重合,点F与点A、B都不重合,可求出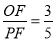 .
.
试题解析:(1)连结CM,则AB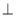 CD,所以OC=0D=4,设⊙M的半径为r,A点的坐标为(-2,0),所以OM=r-2,在Rt△OCM中,
CD,所以OC=0D=4,设⊙M的半径为r,A点的坐标为(-2,0),所以OM=r-2,在Rt△OCM中,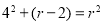 ,所以r=5;(2)因为AB
,所以r=5;(2)因为AB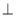 CD,所以弧AC=弧AD,又C为弧AE的中点,所以弧CD=弧AE,所以AE=CD=8;(3)如图2,连结AM,则DM
CD,所以弧AC=弧AD,又C为弧AE的中点,所以弧CD=弧AE,所以AE=CD=8;(3)如图2,连结AM,则DM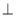 PD, DO
PD, DO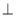 PM,所以△MOD∽△MDP, △MOD∽△DOP ,所以
PM,所以△MOD∽△MDP, △MOD∽△DOP ,所以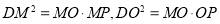 ,所以
,所以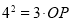 ,所以OP=
,所以OP=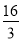 ,然后分三种情况讨论:点F与点A重合时,
,然后分三种情况讨论:点F与点A重合时, ,点F与点B重合时,
,点F与点B重合时, ,点F与点A、B都不重合时,
,点F与点A、B都不重合时,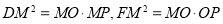 ,所以
,所以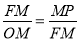 ,因为∠AMF=∠MPF,所以△MFO∽△MPF,所以
,因为∠AMF=∠MPF,所以△MFO∽△MPF,所以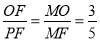 .综上所述
.综上所述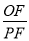 的值不变,值为
的值不变,值为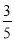 .
.
考点:1.垂径定理;2.勾股定理;3.相似三角形的判定与性质.

某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件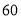 元.经市场调研发现:该款工艺品每天的销售量
元.经市场调研发现:该款工艺品每天的销售量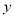 件与售价
件与售价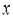 元之间存在着如下表所示的一次函数关系.
元之间存在着如下表所示的一次函数关系.
售价 | … |
|
| … |
销售量 | … |
|
| … |
(1)求销售量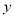 件与售价
件与售价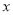 元之间的函数关系式;
元之间的函数关系式;
(2)设每天获得的利润为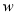 元,当售价
元,当售价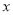 为多少时,每天获得的利润最大?并求出最大值.
为多少时,每天获得的利润最大?并求出最大值.
 元
元


