Question

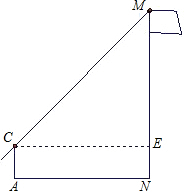
如图，在Rt△ABC中，∠A=90°，AB=AC=8

6

，点E为AC的中点，点F在底边BC上，且FE⊥BE，则△CEF的面积是（　　）

A．16

B．18

C．6 6

D．7 6

Answer 1

过点E作ED⊥BC交BC于点D．
设EF的长为x，
在Rt△ABC中，∠A=90°，AB=AC=8

6

，点E为AC的中点，
∴BC=16

3

，BE=

(8 6 )2+( 1 2 ×8 6 )2

=4

30

，
S_△BCE=

1

2

S_△ABC=

1

2

×

1

2

AB×AC=96，
∵S_△BCE=

1

2

BC×ED，
∴ED=4

3

．
在△BEF中，S_△BEF=

1

2

BE×EF=

1

2

BF×ED，即4

30

x=

(4 30 )2+x2

×4

3

，
解得：x=

4 30

3

，BF=

(4 30 )2+( 4 30 3 )2

=

40 3

3

，
∴CF=BC-BF=

8 3

3

，
∴S_△CEF=

1

2

CF×ED=

1

2

×

8 3

3

×4

3

=16．
故选A．