题目内容
如图,线段AB=10,直线l∥AB,且与AB的距离为8,P是l上一点,PA交以AB为直径的半圆于点C,连结BC、PB.
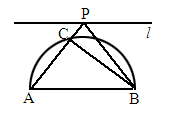
(1)求 ABP的面积;
ABP的面积;
(2)设PA=x,BC=y,求y与x的函数解析式,并求出自变量x的取值范围.
(3)求当4<y<8时,x的取值范围.
答案:40;y=80/x,x>8;10解析:
提示:
|
(1) (2) ∴∠ ACB=90°,∴  , ,
∴  , ,
∴  . .
由于点 P是l上一个动点,AP于半圆交于点C,所以AP必须大于l到AB的距离,故自变量x的取值范围是x>8.(3) 利用图像,当y=4时,x=20,当y=8时,x=10,由图可知10<x<20.
|
提示:
|
 的面积可求;另一方面,由于AB是直径,故∠ACB=90°,AP与BC互相垂直, 的面积可求;另一方面,由于AB是直径,故∠ACB=90°,AP与BC互相垂直, 的面积还可用 的面积还可用 来求,由面积相等可得出y与x的函数解析式. 来求,由面积相等可得出y与x的函数解析式. |

练习册系列答案
相关题目





 12、如图,线段AB、BD、AD围成一个三角形,线段AB、BE、AE也围成一个三角形,那么图中所有线段能围成
12、如图,线段AB、BD、AD围成一个三角形,线段AB、BE、AE也围成一个三角形,那么图中所有线段能围成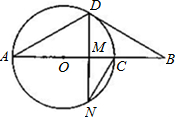 如图,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,∠A=∠B=30°.
如图,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,∠A=∠B=30°. 如图,☉O直径AB=10,C为☉o上一点,AC=6,弦CG平分∠ACB交AB于点D,DE∥BC,DF∥AC,分别次AC、BC于点E、F.
如图,☉O直径AB=10,C为☉o上一点,AC=6,弦CG平分∠ACB交AB于点D,DE∥BC,DF∥AC,分别次AC、BC于点E、F.