题目内容
已知,如图,菱形ABCD,对角线AC=6 cm,BD=8 cm,点P从点A出发沿线段AD向点D运动(不与点A、D重合),速度为1cm/秒;同时,点E从点C出发沿CA向点A运动,速度为![]() cm/秒,过点E作EF∥CD交BD于点F.设点P运动了x秒.
cm/秒,过点E作EF∥CD交BD于点F.设点P运动了x秒.

(1)用含x的代数式填空:PD=________cm,AE=________cm.
(2)当x为何值时△AEP和△OEF相似.
(3)当2.5<x<5时,设S△AEP+S△PEF=ycm2,求y关于x的函数解析式.
(4)以O为原点建立直角坐标系,是否存在抛物线同时过点A、E、F、P,若存在,直接写出x的值,若不存在,说明理由.
答案:
解析:
解析:
|
解:(1)5-x (2)∵EF∥CD ∴∠FEO=∠DCO 又∵∠DAO=∠DCO ∴∠FEO=∠DAO ∴当∠APE=90°或∠AEP=90°时有△AEP和△OEF相似 当∠APE=90°时, ∴ ∴ 当∠AEP=90°时, ∴ ∴ ∴当 (3)当 ∵ ∴ ∴ ∴ ∵ ∴ ∴ (4) (注:当PF∥AE时,得
|

练习册系列答案
相关题目



 ,∴
,∴
 17、已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为
17、已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为
 22、已知:如图,菱形ABCD中,E、F分别是AB、AD上的点,且AE=AF.
22、已知:如图,菱形ABCD中,E、F分别是AB、AD上的点,且AE=AF.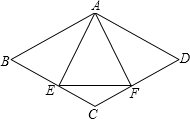 已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;
已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF; (2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.
(2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.