Question

如图，⊙O为△ABC的内切圆，∠C=90°，AO的延长线交BC于D，AC=4，CD=1，则⊙O的半径等于______．

Answer 1

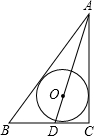
假设半径为r，设切点为E、F，连接OE、OF．
∵OE∥BC，
∴∠AOE=∠ODF，
∴△DFO∽△OEA，
∴

OF

AE

=

DF

OE

即

r

4-r

=

1-r

r

，
解得r=0.8．
故答案为0.8．