Question

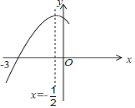
【题目】如图，抛物线＝与轴交于点，其对称轴为直线，结合图象分析下列结论：

① ； ② ；

③ ＞0； ④当时，随的增大而增大；

⑤ ≤（m为实数），其中正确的结论有（ ）

A.2个B.3个C.4个D.5个

Answer 1

【答案】B

【解析】

根据题意和函数图象中的数据，利用二次函数的性质可以判断各个小题中的结论是否正确，从而可以解答本题．

∵抛物线y=ax2+bx+c（a≠0）与x轴交于点（-3，0），其对称轴为直线，

∴抛物线y=ax2+bx+c（a≠0）与x轴交于点（-3，0）和（2，0），且=，

∴a=b，

由图象知：a<0，c>0，b<0，

∴abc>0，故结论①正确；

∵抛物线y=ax2+bx+c（a≠0）与x轴交于点（-3，0），

∴9a-3b+c=0，

∵a=b，

∴c=-6a，

∴3a+c=-3a>0，故结论②正确；

∵当时，y=>0，

∴＜0，故结论③错误；

当x＜时，y随x的增大而增大，当<x<0时，y随x的增大而减小，故结论④错误；

∵a=b，

∴≤可换成≤，

∵a＜0，

∴可得≥-1，

即4m2+4m+1≥0

（2m+1）2≥0，故结论⑤正确；

综上：正确的结论有①②⑤，

故选：B．