题目内容
如图△ABC中,∠C=90°,∠A=30°,B C=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
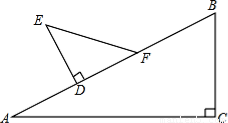
(1) 当△DEF移动至什么位置,即AD的长为多少时,E、B的连线与AC平行.
(2) 在△DEF的移动过程中,是否存在某个位置,使得∠EBD=22.5°?如果存在,求出AD的长度;如果不存在,请说明理由.
(1)  cm;(2)
cm;(2) cm.
cm.
【解析】
试题分析:(1)因为∠C=90°,∠A=30°,BC=5cm,所以AB=10cm,又因为∠FDE=90°,∠DEF=45°,DE=3cm,所以DE=4cm,连接EB,设BE∥AC,则可求证∠EBD=∠A=30°,故AD的长度可求;
(2)当∠EBD=22.5°时,利用三角形外角的性质求得∠BEF=22.5°,则∠EBD=∠BEF,故BF=EF= ,AD=BD-BF-DF=
,AD=BD-BF-DF= (cm);
(cm);
试题解析:(1) cm时,BE∥AC.理由如下:
cm时,BE∥AC.理由如下:
设EB∥AC,则∠EBD=∠A=30°,
∴在Rt△EBD中, cm
cm
∴ cm
cm
∴ cm时,BE∥AC;
cm时,BE∥AC;
(2) 在△DEF的移动过程中,当AD= cm时,使得∠EBD=22.5°.理由如下:
cm时,使得∠EBD=22.5°.理由如下:
假设∠EBD=22.5°.
∵在△DEF中,∠D=90°,∠DEF=45°,DE=3cm,
∴EF= cm,∠DEF=∠DFE=45°,DE=DF=3cm.
cm,∠DEF=∠DFE=45°,DE=DF=3cm.
又∵∠DFE=∠FEB+∠FBE=45°,
∴∠EBD=∠BEF,
∴BF=EF= ,
,
∴AD=BD-BF-DF= (cm).
(cm).
∴在△DEF的移动过程中,当AD= cm时,使得∠EBD=22.5°.
cm时,使得∠EBD=22.5°.
考点: 几何变换综合题

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案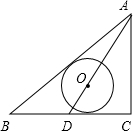 如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )
如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )A、
| ||
B、
| ||
C、
| ||
| D、2 |
 8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为
8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为 (2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于
(2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于 如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为
如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为 如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.
如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.