题目内容
 如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为
如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为
- A.3
- B.

- C.4
- D.
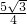
B
分析:根据三角函数求出点B的坐标,代入直线y=x+b(b>0),即可求得b的值.
解答: 解:由直线y=x+b(b>0),可知∠1=45°,
解:由直线y=x+b(b>0),可知∠1=45°,
∵∠α=75°,
∴∠ABO=180°-45°-75°=60°,
∴OB=OA÷tan∠ABO= .
.
∴点B的坐标为(0, ),
),
∴ =0+b,b=
=0+b,b= .
.
故选B.
点评:本题灵活考查了一次函数点的坐标的求法和三角函数的知识,注意直线y=x+b(b>0)与x轴的夹角为45°.
分析:根据三角函数求出点B的坐标,代入直线y=x+b(b>0),即可求得b的值.
解答:
 解:由直线y=x+b(b>0),可知∠1=45°,
解:由直线y=x+b(b>0),可知∠1=45°,∵∠α=75°,
∴∠ABO=180°-45°-75°=60°,
∴OB=OA÷tan∠ABO=
 .
.∴点B的坐标为(0,
 ),
),∴
 =0+b,b=
=0+b,b= .
.故选B.
点评:本题灵活考查了一次函数点的坐标的求法和三角函数的知识,注意直线y=x+b(b>0)与x轴的夹角为45°.

练习册系列答案
相关题目
 如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )| A、3 | ||||
B、
| ||||
| C、4 | ||||
D、
|

 C.4 D.
C.4 D.








