Question

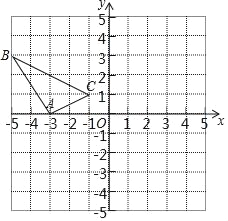
【题目】如图，等边△OAB的边长为2，以它的顶点O为原点，OB所在的直线为x轴，建立平面直角坐标系.若直线y=x+b与△OAB的边界总有两个公共点，则实数b的范围是____.

Answer 1

【答案】

【解析】

由题意，可知点A坐标为（1，），点B坐标为（2，0），由直线与△OAB的边界总有两个公共点，有截距b在线段CD之间，然后分别求出点C坐标和点D坐标，即可得到答案.

解：如图，过点A作AE⊥x轴，

.∵△ABC是等边三角形，且边长为2，

∴OB=OA=2，OE=1，

∴，

∴点A为（1，），点B为（2，0）；

当直线经过点A（1，）时，与△ABC边界只有一个交点，

则，解得：，

∴点D的坐标为（）；

当直线经过点B（2，0）时，与△ABC边界只有一个交点，

则，解得：，

∴点C的坐标为（0，）；

∴直线与△OAB的边界总有两个公共点时，截距b在线段CD之间，

∴实数b的范围是：；

故答案为：.