题目内容
16.计算:(1)$\frac{1}{2m}-\frac{1}{m+n}•(\frac{m+n}{2m}-m-n)$
(2)先化简,再求值$(\frac{1}{x+y}+\frac{1}{y-x})÷\frac{y^2}{{xy-{y^2}}}$,其中x=-2,y=1.
分析 (1)乘法利用乘法分配律计算,再进一步计算得出答案即可即可;
(2)先计算括号的加法,然后把除法转换为乘法把分式化简,再把数代入求值.
解答 解:(1)$\frac{1}{2m}-\frac{1}{m+n}•(\frac{m+n}{2m}-m-n)$
=$\frac{1}{2m}$-($\frac{1}{2m}$-1)
=$\frac{1}{2m}$-$\frac{1}{2m}$+1
=1;
(2)原式=-$\frac{2y}{(x+y)(x-y)}$•$\frac{y(x-y)}{{y}^{2}}$
=$-\frac{2}{x+y}$,
当x=-2,y=1时,原式=-$\frac{2}{-2+1}$=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.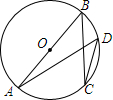 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
8. 如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
 如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )| A. | 3.40×102 | B. | 340×104 | C. | 3.40×104 | D. | 3.40×106 |
6.代数式-2x,0,3x-y,$\frac{x+y}{4}$,$\frac{x}{π}$中,单项式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
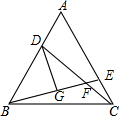 已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:
已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证: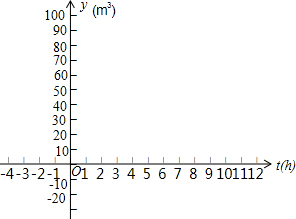 某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.
某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.
 中秋节期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成三个面积相等的扇形,三个扇形区域里分别标有“10元”、“20元”、“30元”的字样(如图).规定:同一天内,顾客在本商场每消费满100元,就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券.某顾客当天消费240元,转了两次转盘.
中秋节期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成三个面积相等的扇形,三个扇形区域里分别标有“10元”、“20元”、“30元”的字样(如图).规定:同一天内,顾客在本商场每消费满100元,就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券.某顾客当天消费240元,转了两次转盘.