题目内容
若a,b,c分别是三角形的三边,判断方程(a+b)x2+2cx+(a+b)=0的根的情况.
考点:根的判别式,三角形三边关系
专题:
分析:先求出△=b2-4ac的值,再根据三角形的三边关系分别进行判断,即可得出答案.
解答:解:△=(2c)2-4(a+b)(a+b)=4c2-4(a+b)2=4(c+a+b)(c-a-b).
∵a,b,c分别是三角形的三边,
∴a+b>c.
∴c+a+b>0,c-a-b<0,
∴△<0,
∴方程没有实数根.
∵a,b,c分别是三角形的三边,
∴a+b>c.
∴c+a+b>0,c-a-b<0,
∴△<0,
∴方程没有实数根.
点评:本题主要考查了一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
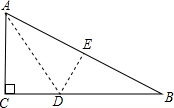 如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A、2cm | B、3cm |
| C、4cm | D、5cm |