题目内容
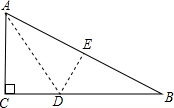 如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A、2cm | B、3cm |
| C、4cm | D、5cm |
考点:翻折变换(折叠问题)
专题:
分析:首先根据题意得到:△AED≌△ACD;进而得到AE=AC=6,DE=CD;根据勾股定理求出AB=10;再次利用勾股定理列出关于线段CD的方程,问题即可解决.
解答: 解:
解:
由勾股定理得:
AB=
=
=10,
由题意得:△AED≌△ACD,
∴AE=AC=6,DE=CD(设为x);
∠AED=∠C=90°,
∴BE=10-6=4,BD=8-x;
由勾股定理得:
(8-x)2=42+x2,
解得:x=3(cm),
故选B.
 解:
解:由勾股定理得:
AB=
| 62+82 |
| 100 |
由题意得:△AED≌△ACD,
∴AE=AC=6,DE=CD(设为x);
∠AED=∠C=90°,
∴BE=10-6=4,BD=8-x;
由勾股定理得:
(8-x)2=42+x2,
解得:x=3(cm),
故选B.
点评:该命题主要考查了翻折变换及其应用问题;解题的关键是借助翻折变换的性质,灵活运用勾股定理、全等三角形的性质等几何知识来分析、判断、推理或解答.

练习册系列答案
相关题目
计算cos80°-sin80°的值大约为( )
| A、0.8111 | B、-0.8111 |
| C、0.8112 |
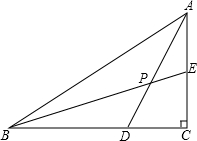 如图,在△ABC中,∠C=90°,D、E分别为BC、AC上一点,BD=AC,DC=AE,BE与AD交于点P,则∠ADC+∠BEC=
如图,在△ABC中,∠C=90°,D、E分别为BC、AC上一点,BD=AC,DC=AE,BE与AD交于点P,则∠ADC+∠BEC=