题目内容
 如图,DE∥BC,∠ADE=60°,∠C=50°,则∠A=
如图,DE∥BC,∠ADE=60°,∠C=50°,则∠A=考点:平行线的性质,三角形内角和定理
专题:
分析:先根据平行线的性质求出∠B的度数,再由三角形内角和定理即可得出结论.
解答:解:∵DE∥BC,∠ADE=60°,
∴∠B=∠ADE=60°.
∵∠C=50°,
∴∠A=180°-60°-50°=70°.
故答案为:70°.
∴∠B=∠ADE=60°.
∵∠C=50°,
∴∠A=180°-60°-50°=70°.
故答案为:70°.
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列运算中,正确的是( )
| A、a2+a2=a4 |
| B、(a-b)2=a2-b2 |
| C、-a(1-a)=a2-a |
| D、a3•a-4=a-12 |
比较-2.4,+(-0.5),-(-2),-|-3|的大小,下列正确的是( )
| A、-|-3|>-2.4>-(-2)>+(-0.5 ) |
| B、-(-2)>-|-3|>-2.4>+(-0.5) |
| C、-(-2)>+(-0.5)>-2.4>-|-3| |
| D、-|-3|>-(-2)>-2.4>+(-0.5) |
已知方程(x+1)(x-1)=(x-1),则x的值为( )
| A、-1 | B、1或0 |
| C、0 | D、-1或0 |
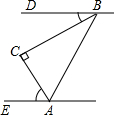 如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=70°,则∠DBC的度数是( )
如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=70°,则∠DBC的度数是( )| A、20° | B、40° |
| C、50° | D、70° |
已知|a+13|+|b-10|=0,则a+b的值是( )
| A、-3 | B、3 | C、23 | D、-23 |
 如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为
如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为