题目内容
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线 交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值( )
交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值( )
| A.等于2 | B.等于 | C.等于 | D.无法确定 |
B
解析试题分析:先设出B点坐标,即可表示出C点坐标,根据三角形的面积公式和反比例函数的几何意义即可解答.
解:方法1:设B点坐标为(a,b),
∵OD:DB=1:2,
∴D点坐标为( a,
a, b),
b),
根据反比例函数的几何意义,
∴ a•
a• b=k,
b=k,
∴ab=9k①,
∵BC∥AO,AB⊥AO,C在反比例函数y= 的图象上,
的图象上,
∴设C点横坐标为m,
则C点坐标为(m,b)
将(m,b)代入y= 得,
得,
m= ,
,
BC=a﹣ ,
,
又因为△OBC的高为AB,
所以S△OBC= (a﹣
(a﹣ )•b=3,
)•b=3,
所以 (a﹣
(a﹣ )•b=3,
)•b=3,
(a﹣ )b=6,
)b=6,
ab﹣k=6②,
把①代入②得,
9k﹣k=6,
解得k= .
.
方法2:延长BC交y轴于E,过D作x轴的垂线,垂足为F.
由△OAB的面积=△OBE的面积,△ODF的面积=△OCE的面积,
可知,△ODF的面积= 梯形DFAB=
梯形DFAB= △BOC的面积=
△BOC的面积= ,
,
即 k=
k= ,
,
k= .
.
故选B.
考点:反比例函数系数k的几何意义.
点评:本题考查了反比例系数k的几何意义.此题还可这样理解:当满足OD:DB=1:2时,当D在函数图象上运动时,面积为定值.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
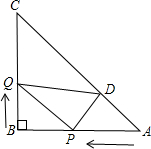 点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s.
点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s. (2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为
(2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为