题目内容
 梯形ABCD,AD∥BC,∠A=90°AB=8cm,AD=24cm,BC=26cm点,点P从A出发沿线段AD的方向以1cm/s的速度运动;点Q从C出发沿线段CB的方向以3cm/s的速度运动,点P、Q分别从A、C同时出发,当点P运动到点D时,点Q随之停止运动.设运动时间为t(秒).
梯形ABCD,AD∥BC,∠A=90°AB=8cm,AD=24cm,BC=26cm点,点P从A出发沿线段AD的方向以1cm/s的速度运动;点Q从C出发沿线段CB的方向以3cm/s的速度运动,点P、Q分别从A、C同时出发,当点P运动到点D时,点Q随之停止运动.设运动时间为t(秒).(1)设四边形PQCD的面积为S,写出S与t之间的函数关系(注明自变量的取值范围);
(2)当t为何值时,四边形PQCD为等腰梯形?
分析:(1)根据条件可以得出S四边形PQCD=S梯形ABCD-S梯形ABQP就可以得出S与t之间的函数关系式;
(2)如图2,当四边形PQCD是等腰梯形,作DF∥PQ交BC于F,就可以得出DP=QF=3t-4,从而建立方程求出其解即可.
(2)如图2,当四边形PQCD是等腰梯形,作DF∥PQ交BC于F,就可以得出DP=QF=3t-4,从而建立方程求出其解即可.
解答:解:(1)AD=24,BC=26,AB=8,AP=t,CQ=3t,
BQ=BC-CQ=26-3t
S四边形PQCD=S梯形ABCD-S梯形ABQP,
S=200-104+8t=8t+96(0<t≤
)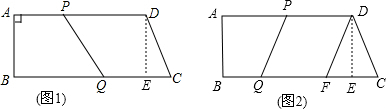
(2)如图2,当四边形PQCD是等腰梯形,作DF∥PQ交BC于F,作DE⊥BC于E,
∴四边形PQFD是平行四边形,四边形ABED是矩形
∴PQ=DF=CD,AD=BE=24
∴△DFC是等腰三角形,EC=2
∴FC=2CE=4.
∵QC=PD+2(BC-AD)
∴3t=24-t+4
∴t=7.
答:t=7时,四边形PQCD为等腰梯形.
BQ=BC-CQ=26-3t
S四边形PQCD=S梯形ABCD-S梯形ABQP,
S=200-104+8t=8t+96(0<t≤
| 26 |
| 3 |

(2)如图2,当四边形PQCD是等腰梯形,作DF∥PQ交BC于F,作DE⊥BC于E,
∴四边形PQFD是平行四边形,四边形ABED是矩形
∴PQ=DF=CD,AD=BE=24
∴△DFC是等腰三角形,EC=2
∴FC=2CE=4.
∵QC=PD+2(BC-AD)
∴3t=24-t+4
∴t=7.
答:t=7时,四边形PQCD为等腰梯形.
点评:本题考查了梯形的面积公式的运用,等腰三角形的性质的运用,矩形的性质的运用,解答时根据动点问题的图形变化灵活运用四边形的性质求解是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
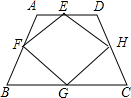 如图,已知等腰梯形ABCD,AD∥BC,AB=DC,E、F、G、H 分别是AD、AB、BC、CD的中点,则四边形EFGH一定是( )
如图,已知等腰梯形ABCD,AD∥BC,AB=DC,E、F、G、H 分别是AD、AB、BC、CD的中点,则四边形EFGH一定是( )| A、正方形 | B、矩形 | C、菱形 | D、等腰梯形 |
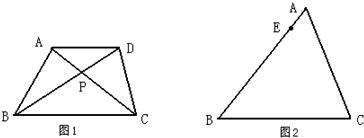

 如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.
如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.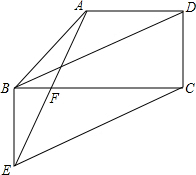 如图,梯形ABCD,AD∥BC,连接BD,过B、C分别作CD、BD的平行线交于E,连接AE交BC于F,求证:F是AE的中点.
如图,梯形ABCD,AD∥BC,连接BD,过B、C分别作CD、BD的平行线交于E,连接AE交BC于F,求证:F是AE的中点.