题目内容
如图,PA,PB分别与⊙O相切于A,B两点,∠ACB=60°.
(1)求∠P的度数;
(2)若⊙O的半径长为4cm,求图中阴影部分的面积.

解:连接OA、OB,
∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°,
又∵∠AOB=2∠C=120°,
∴∠P=360°﹣(90°+90°+120°)=60°.
∴∠P=60°.
(2)连接OP,
∵PA、PB是⊙O的切线,
∴ APB=30°,
APB=30°,
在RT△APO中,tan30°= ,
,
∴AP= =
= =4
=4 cm,
cm,
∴S阴影=2S△AOP﹣S扇形=2×( ×4×
×4× ﹣
﹣ )=(16
)=(16 ﹣
﹣ )(cm2).
)(cm2).


练习册系列答案
相关题目
 D在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:
D在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据: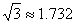 ,
,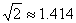 .结果保留整数).
.结果保留整数).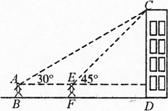
 =
= .
. 的倒数为( )
的倒数为( ) 的绝对值是 ,
的绝对值是 , B. 4或5 C. 5或6 D. 6
B. 4或5 C. 5或6 D. 6