题目内容
如图,△ABC中,∠BAC=90°,正方形的一边GF在BC上,其余两个顶点D,E分别在AB,AC上.连接AG,AF分别交DE于M,N两点.
(1)求证: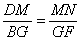 .
.
(2) 求证: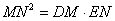 .
.
(3)若AB=AC=2,求MN的
(1)证明:∵四边形DGFE是正方形,∴DN∥BF,
∴△ADM∽△ABG,
∴ ,同理可得
,同理可得 .
.
∴ .
.
(2)证明:由(1)可知 ,同理也可以得到
,同理也可以得到 ,
,
∴ ,
, .-
.-
∵∠B+∠C=90°,∠CEF+∠C=90°. ∴∠B=∠CEF,
又∵∠BGD=∠EFC=Rt∠,∴△BGD∽△EFC. ∴ .
.
∵DG,GF,EF是同一个正方形的边长,∴DG=GF=EF. ∴
∴ , ∴MN 2=DM·EN -
, ∴MN 2=DM·EN -
(3) ∵ ∴
∴
∵∠B=∠C=45o , 四边形DEFG是正方形,
∴
∵ 由(1)(2)可得
∴

练习册系列答案
相关题目
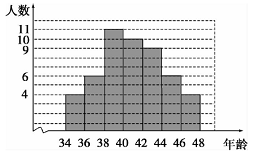
王明同学随机抽某市10个小区所得到的绿化率情况,结果如下表:
| 小区绿化率(%) | 20 | 25 | 30 | 32 |
| 小区个数 | 2 | 4 | 3 | 1 |
则关于这10个小区的绿化率情况,下列说法错误的是( )
A.极差是13% B.众数是25% C.中位数是25% D.平均数是26.2%

 ≈1.4,
≈1.4, ≈1.7)
≈1.7)
 轴的正半轴上。现将线段OA绕点O逆时针旋转
轴的正半轴上。现将线段OA绕点O逆时针旋转 度,且
度,且 。
。 上;
上; 上,则
上,则 的取值范围是 .
的取值范围是 . 和
和 ,则通过比较线段OC与CD的大小,可以得到关于正数
,则通过比较线段OC与CD的大小,可以得到关于正数 B、
B、
 D、
D、

 = .
= .
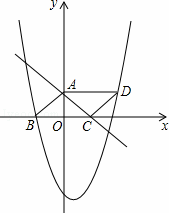
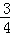 x+3的图象与y,x轴的交点,点B在二次函数
x+3的图象与y,x轴的交点,点B在二次函数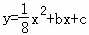 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形。
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形。