题目内容
如图,在△A BC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2 cm,AD=4 cm.
BC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2 cm,AD=4 cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
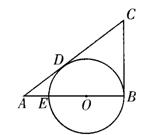
解:(1)连接OD ∴OD⊥AC
∴△ODA是Rt△
设半径为r ∴AO=r+2 ∴(r+2)2—r2=16
解之得:r=3 ∴BE=6
(2) ∵∠ABC=900 ∴OB⊥BC ∴BC是⊙O的切线
∵CD切⊙O于D ∴CB=CD 令CB=x
∴AC=x+4,BC=4,AB=x,AB=8 ∵ ∴
∴
∴S△ABC=

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 C.50° D.60°
C.50° D.60°
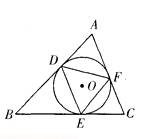 如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( )
如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( )  条中线的交点
条中线的交点
 = ( )
= ( )
 剪去
剪去 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ( )
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ( )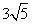 cm
cm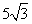 cm
cm

