题目内容
要测量河两岸相对的A，B两点间的距离，先从B点出发，与AB成90°角方向向前走100m到C处，在C处立一根标杆，然后方向不变继续朝前走25m到D处，在D处转90°，沿DE方向走12m到达E处，使A（目标），C（标杆）与E在同一直线上，求A，B之间的距离．
解：∵∠ABC=∠EDC=90°，∠ACB=∠ECD，
∴△ABC∽△EDC，
∴
=
，
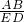则AB=•ED=
×12=48，
即AB之间的距离为48m．
分析：根据∠ABC=∠EDC=90°，∠ACB=∠ECD，证明△ABC∽△EDC，然后根据对应边成比例求出AB的长度即可．
点评：本题考查了相似三角形的应用，难度适中，解题的关键是根据三角形的相似得出对应边成比例．
∴△ABC∽△EDC，
∴
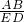=，则AB=
•ED=×12=48，即AB之间的距离为48m．
分析：根据∠ABC=∠EDC=90°，∠ACB=∠ECD，证明△ABC∽△EDC，然后根据对应边成比例求出AB的长度即可．
点评：本题考查了相似三角形的应用，难度适中，解题的关键是根据三角形的相似得出对应边成比例．
练习册系列答案
相关题目
12、如图，要测量河两岸相对的两点A，B的距离，在AB的垂线BF上取两点C，D，使BC=CD，再定出BF的垂线DE，使A，C，E在一条直线上，这时测得DE=16米，则AB=
4、如图，要测量河两岸相对的两点A、B间的距离，先在过B点的AB的垂线L上取两点C、D，使CD=BC，再在过D点的垂线上取点E，使A、C、E在一条直线上，这时，△ACB≌△ECD，ED=AB，测ED的长就得AB得长，判定△ACB≌△ECD的理由是（ ）
如图，要测量河两岸相对的两点A和B的距离，可以在AB的垂线BF上取两点C、D，再作BF的垂线DE，使A、C、E三点在同一直线上．
要测量河两岸相对的A，B两点间的距离，先从B点出发，与AB成90°角方向向前走100m到C处，在C处立一根标杆，然后方向不变继续朝前走25m到D处，在D处转90°，沿DE方向走12m到达E处，使A（目标），C（标杆）与E在同一直线上，求A，B之间的距离．
如图要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，并使点A、C、E三点在同一条直线上，因此只要测得ED的长就知道AB的长．请说明这样测量正确性的理由．