题目内容
【题目】如图，正六边形ABCDEF是边长为2 cm的螺母，点P是FA延长线上的点，在A，P之间拉一条长为12 cm的无伸缩性细线，一端固定在点A，握住另一端点P拉直细线，把它全部紧紧缠绕在螺母上(缠绕时螺母不动)，则点P运动的路径长为（ ）
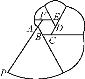
A. 13π cm B. 14π cm C. 15π cm D. 16π cm
【答案】B
【解析】
由题意知，细线正好缠绕螺母一周，故
运动的路径为图中外围一圈从到
的6段弧长，不妨倒过来求，从出发先求最小弧长.正六边形每个内角为
，则每段弧所对的圆心角均为
，且半径分别为
、
、
、
、
、
，代入弧长公式
，再相加即可.
根据题意可知点
运动的路线就是图中六条扇形的弧长，因为正六边形
是边长为
的螺母，故扇形的圆心角为
，半径分别为
，
，
，
，
，，故点运动的路径长为：
.
故选：B
练习册系列答案
精英口算卡系列答案
相关题目
【题目】如下表，方程1、方程2、方程3…是按照一定规律排列的一列方程。
（1）猜想方程1的解，并将它们的解填在表中的空白处。
序号 | 方程 | 方程的解（ |
1 |
|
|
2 |
|
|
3 |
|
|
… | …… | …… |
（2）若方程
的解是
，猜想a,b的值。
（3）请写出这列方程中的第n个方程和它的解。
